수치해석
재료공학도를 위한 수치해석
Orientation
- 국립창원대학교 재료금속공학과
- 실습 환경
- VScode + Jupyter
- GitHub 계정을 만들고 결합하길 권함.
- Windows, MacOS, Linux 등 다양한 컴퓨터 환경에서 실습 가능함.
- 구글 계정을 활용해서 Google Colab과 Google Drive을 결함한 형태로 Cloud service를 활용해서, 인터넷 연결된 웹브라우저를 활용해서 실습 가능하나 추천하진 않음.
수업 목표
- 기초 수치해석을 이해하고, Python 등의 프로그램을 활용해 수치해석에 활요할 수 있다.
Week1
수업 01-1 (오리엔테이션)
- 대상
- 국립창원대학교 재료금속공학과 2학년 학생
- 수치해석은 전공필수 교과로써 반드시 이수하여야만 졸업 가능
- 수업을 원활히 이해하기 위해서는 mse_data 강의를 선수강할 필요 있음
- 준비물
- 강의자료는 여기에서 찾을 수 있음
- 개인용 컴퓨터
- 노트
- 수업자료 출력물
- Python, Jupyter notebook 등에 대한 기본적 이해와 활용 능력
- Numpy, Matplotlib 등 주요 Python library에 대한 이해와 활용 능력
- pip 활용해서 필요한 패키지를 제때 설치할 수 있어야 함.
- 평가
- 출석 (50%) - 출석이 매우 중요 - 앞선 주차의 내용을 이해 못하면 중도 탈락하게 됨 반드시 빠지지 않고 참석해야 함
- 태도 점수, 참여가 저조하거나, 뒷자리 앉아서 수업에 참여하지 않으면 F
- 강의에 필요한 준비물이 갖춰져 있지 않으면 출석 인정 안됨
- 중간 / 기말 평가
- 강의 내용에 대한 이론 평가
- 강의 내용을 스스로 프로그램/디버깅 하여 만들 수 있어야 함.
- 강의
- 수치해석은 전공필수 입니다. F학점으로는 졸업이 불가능합니다.
- 반드시 스스로 실습해야함. 증명뿐만 아니라, 컴퓨터 코딩까지 스스로해야 함.
수업 01-2 (수치해석 전반 설명)
Week2
수업 02-1 (수와 오차 Error)
- 컴퓨터의 수
- 컴퓨터가 다루는 수에는 항상 오차가 있다. (한정된 메모리)
- 수의 종류
- 정수 (integer): …, -2, -1, 0, 1, 2, …
- 유리수 (rational): 분수로 나타낼 수 있는 수 (1/2, 2/3, 0.5, …)
- 무리수 (irrational): 소수로 끝없이 이어지는 수 (3.141592… , 1.414213…, Euler’s number)
import numpy as np print('pi:',np.pi) # 내 컴퓨터에서는 3.141592653589793 까지만 출력되었다. # 여러분들 컴퓨터는 어떤가? print('Euler number:',np.exp(1)) # 마찬가지로 2.718281828459045 까지만 출력되었다.
- 오차의 종류
- (1) 반올림 오차 (round-off error). 메모리가 유한하므로, 유한한 자리수까지만 저장한다. 예:
0.3333..을 소수점 네자리까지만 저장하면 0.3333이 되고, 진짜 값과 ‘오차’가 생깁니다.a = 0.1 + 0.2 print(a) # 0.30000000000000004위 예시에서, 컴퓨터는 2진법으로 수를 저장하다 보니, 정확히 0.3이 계산되지 않고, 오차가 생깁니다.
-
(2) 절단 오차 (truncation error) 무한한 계산 과정을 중간에 끊어서 근사(approximation)할 때 생기는 오차에요. 예를 들어, Taylor급수로 \(\sin{x}\)를 표현하면,
\[\sin x= \sum_{n=0}^\infty\frac{(-1)^n}{(2n+1)!}x^{2n+1}\]따라서 만약 n=0,..,3까지만 전개해보면 아래와 같다.
\[\sin x\approx \frac{1}{1!}x^1 +\frac{-1^1}{3!}x^3 +\frac{(-1)^2}{5!}x^5 +\frac{-1^3}{7!}x^7\]우선 Factorial을 구현할 Python 함수를 구해보자.
def factorial(x): val=1 for i in range(1,x+1): val=val*i return val ## Test factorial function for i in range(1,4): print(f'{i}! = {factorial(i)}')실은 math library에 이미 factorial 함수가 존재한다.
import math math.factorial(3)그 다음으로 테일러 급수를 함수로 표현해보면…
def sinx_taylor(x,fin): val=0. for n in range(0,fin+1): term=(-1)**n/(factorial(2*n+1))*(x**(2*n+1)) # print(f'{n}-th term: {term}') val+=term return val- 테일러 항 차수에 따라 달라지는 오차의 변화를 살펴보자.
- n값의 변화에 따라서,
- 여러 x값에서 Taylor 급수와의 차이값을 그려보자.
import matplotlib.pyplot as plt import numpy as np xs=np.linspace(-1.5*np.pi,1.5*np.pi) plt.plot(xs,np.sin(xs),label='actual') for n in range(2,10): ys=sinx_taylor(xs,n) plt.plot(xs,ys,label=f'Taylor series n={n}') plt.legend() plt.xlim(-4,4) plt.ylim(-2,2)
-
에제: \(y=e^x\)
이 함수의 테일러 시리즈는 다음과 같다: \(e^x=\sum_{n=0}^{\infty}\frac{1}{n!}x^n\)
-
\(n=4\)까지 전개 하면:
\[e^x=1+x+1/2x^2+1/6x^3+1/24x^4 ...\] -
이 둘을 직접 그려보고 얼마나 유사한지 살펴보자
def taylor_ex(x,n): s=0. for i in range(0,n+1): s=s+1./factorial(i)*(x**i) return s xs=np.linspace(0,3) plt.plot(xs,np.exp(xs),'k-',label=r'$y=e^x$',lw=3,alpha=0.3) for n in range(1,6): plt.plot(xs,taylor_ex(xs,n), #continued '--',label=rf'Taylor series up to $n=${n}') plt.ylim(0,20) plt.legend() -
-
에제: \(y=\cos(x)\)의 테일러 급수를 사용해서 \(n=1,4,7,10\)까지 경우를 나타내고 실제 y=cos(x)함수와의 차이를 비교해보자.
-
예제: \(y=\ln(1+x)\) 여기서 \(x\)의 범위는 \(x\in(-1,1]\)
- 예제: Maclaurin series expansion for chemical potential (?)
- 테일러 항 차수에 따라 달라지는 오차의 변화를 살펴보자.
- (1) 반올림 오차 (round-off error). 메모리가 유한하므로, 유한한 자리수까지만 저장한다. 예:
- 오차 측정 방법
-
(1) 절대 오차 (absolute error)
\[E^a=|x^{true}-x^{approx}|\]x_true=3 x_approx=3.5 err_rel= abs(x_true-x_approx) -
(2) 상대 오차 (relative error)
\[E^r=\frac{|x^{true}-x^{approx}|}{|x^{true}|}\]x_true=3 x_approx=3.5 err_rel= abs(x_true-x_approx)/abs(x_true)** 상대 오차를 사용할 수 없는 경우는 언제일까?
-
(3) 수열의 오차?
만약 수열 \(\boldsymbol{x}\)가 여러 값으로 이루어진 배열이라면?
각 배열내의 요소의 절대 오차가 아래와 같이 정의되겠다.
\[E_i=|x^{true}_i-x^{approx}_i|\]전체 수열의 오차를 구하면?
\[\sum_iE_i=|x^{true}_i-x^{approx}_i|\]혹은 아래와 같이 표현이 더욱 유용할 수 있겠다.
\[Error=\sqrt{\sum_i(x^{true}_i-x^{approx}_i)^2}\]위와 같은 수열의 오차를 표현하자면 아래와 같다.
import numpy as np # numpy 패키지 활용 x_true =np.array([ 1, 2, 4]) x_approx=np.array([1.3,-1.9,4.3] ) summedup=0. for i in range(len(x_true)): summedup+=(x_true[i]-x_approx[i])**2 error=np.sqrt(summedup) ## 혹은 Numpy의 broadcasting 기능과 .sum() method 활용해 ## 더욱 축약해 아래와 같이 표현할 수 있겠다. error=np.sqrt(((x_true-x_approx)**2).sum()) -
두 벡터
\[\boldsymbol a, \boldsymbol b\]가 서로 얼마나 유사한지 살펴보려면, 아래와 같이 단순한 차로 살펴볼 수 있을까?
\[\boldsymbol a -\boldsymbol b=?\]위의 결과는 scalar가 아닌 또 다른 벡터의 결과로 이어진다.
앞서 수열에 대한 오차를 표기했듯 아래 표현이 더 적절하겠다.
\[Error=\sqrt{(a_1-b_1)^2+(a_2-b_2)^2+(a_3-b_3)^2}\]혹은 위의 수열에 대한 오차를 표기했듯
\[Error=\sqrt{\sum_i^3(a_i-b_i)^2}\]라 표기할 수 있겠다. 그리고 이는 더욱 축약하자면
\[Error=|\boldsymbol a- \boldsymbol b|\]와 같이 표기할 수 있겠다.
만약 상대 오차를 구한다면?
\[Error=\frac{|\boldsymbol a- \boldsymbol b|}{0.5(|\boldsymbol a|+|\boldsymbol b|)}\]혹은 더욱 명백하게 인덱스 notation을 활용해 표현하자면 아래와 같이 나타낼 수 있다.
\[Error=\frac{\sqrt{(a_1-b_1)^2+(a_2-b_2)^2+(a_3-b_3)^2}}{0.5\big(\sqrt{a_1^2+a_2^2+a_3^2}+\sqrt{b_1^2+b_2^2+b_3^2}\big)}\]위에 제시된 오차의 정의를 파이썬으로 표현해보자.
import numpy as np def get_abs(v): """ Function that calculates the magnitude of given vector `v` Arguments --------- v Returns ------- the magnitude of given vector v """ return np.sqrt(v[0]**2+v[1]**2+v[2]**2) ## two vectors a=np.array([1. ,2. ,3. ]) b=np.array([1.2,1.9,3.1]) ## absolute error between the two vectors err=get_abs(a-b) print('1 error:',err) ## Relative error between the two vectors err=get_abs(a-b) #분자까지만, err=err/0.5*(get_abs(a)+get_abs(b)) # 분모로 나누면.. print('2 error:',err)
-
수업 02-2 (컴퓨터의 유한 정밀도 (floating point 개념))
- 유한정밀도
- 컴퓨터는 0과 1 (이진수, binary)만 저장할 수 있음.
- 무리수를 비롯한 실수(real number)는 무한히 많은 자리수 (3.141592…)를 가질 수 있으나, 메모리가 한정되어 정해진 비트 수까지만 저장가능함 (32비트, 62비트 등)
- 그로인해 수를 근사치로 저장하고 표현함; 유한한 정밀도를 가짐 (finite precision)
- 부동 소수점 (Float point) (cf. <-> 고정 소수점 (Fixed piont))
- 수를 저장하는 방식 부호(sign), 지수(exponent), 가수(mantisa)를 각각 이진법(0 혹은 1)로 표현함.
- 예 10진수 5.75를 저장하기
- 5 =
101 -
0.75 =
0.110.75를 이진수로 만들기 위해서는 우선 2를 곱한다: \(0.75\times 2 = 1.5\) 실수
1을 제외한 나머지0.5에 다시 2를 곱한다. \(0.5\times 2 = 1.0\) 실수1을 제외한 나머지가 0이 되어 사라질때까지 반복한다. 따라서 5.75 =101.11가 된다. 이 값을 정규화와 부호 및 지수 처리를 한 후 저장. -
정규화(normalization)
IEEE 754에 의하여 항상 수를
\[1.\text{XXXX..} \times 2^n\]형태로 바꿔서 저장함. 따라서 이진수
\[101.11\rightarrow1.\green{0111}\times 2^{\red{2}}\]101.11을 아래와 같이 변환:위와 같이 저장하면 두 부분의 수가 저장되어야 함.
- 가수(mantissa) = \(\green{0111}0000...\) (정해진 칸내에서 유효숫자 뒤는 0으로 채운다.)
- 지수(exponent) = \(\red{2}\)
- base가
2인 이유는 이진법을 활용하기 때문에…
-
부호
5.75는 양수 이므로, 부호는 양수로 저장 (부호비트 이진수 =0) -
지수
IEEE 754에 의하여 지수를 바이어스(bias) 방식으로 저장한다.
- double precision의 바이어스는 = \(\blue{1023}\)
- 실제 지수는: \(\red{2}\).
- 저장되는 지수는: \(\red{2}+\blue{1023}=1025\)
- 따라서 바이어스 처리된 1025를 아래와 같이 2진수로 표현하면?
몫 나머지 --------------------- 1025 / 2 = 512 ... 1 512 / 2 = 256 ... 0 256 / 2 = 128 ... 0 128 / 2 = 64 ... 0 64 / 2 = 32 ... 0 32 / 2 = 16 ... 0 16 / 2 = 8 ... 0 8 / 2 = 4 ... 0 4 / 2 = 2 ... 0 2 / 2 = 1 ... 0 1 / 2 = 0 ... 110000000001가 된다 (11비트, 즉 2진법으로 11자리)
-
가수 (Mantissa, fraction)
정규화된 수 \(1.0111 \times 2^2\)에서 앞의 1은 항상 생략(숨겨진 1), 따라서 저장되는 건 0111 뒤에 0으로 채운 52비트입니다. mantissa = 0111000…0 (52비트)
-
5.75를 IEEE 754 방식으로 저장한다면..- 부호 =
0(1비트, 즉 0(+) 또는 1(-)) - 지수 =
10000000000(11비트) - 가수 =
0111000000000000000000000000000000000000000000000000(52비트) - 따라서 전체는
0100000000000111000000000000000000000000000000000000000000000000
- 부호 =
- 5 =
- 예, 10진수 1.5를 저장하기.
- 1=
1 -
0.5 = ?
\[0.5 \times 2 = 1.0\]실수
1이 나온다. 따라서 0.5=1.1이 된다. -
정규화는?
\[1.\text{XXXX...} \times 2^n\]으로 해야하므로,
\[1.1\rightarrow1.1 \times 2^0\]가수/지수를 구하면
- 가수 = \(10000...\)
- 지수 = 0
- 부호 =0
- 지수는 바이어스로 저장한다 (1023). 따라서
- \[0+1023=1023\]
- 바이어스 처리된 1023을 이진수로 표현하면?
1023/2=511 ... 1 511 /2=255 ... 1 255 /2=127 ... 1 127 /2=63 ... 1 63 /2=31 ... 1 31 /2=15 ... 1 15 /2=7 ... 1 7 /2=3 ... 1 3 /2=1 ... 1 1. /2=0. ... 1따라서
1111111111가 된다.
- 가수 정규화된 수 \(1.1\times 2^0\)에서 앞자리 1은 숨기고, 나머지
1뒤에 0을 채운 52비트. - 총정리하자면
- 부호=
0(1비트) - 지수=
01111111111(11비트) - 가수=
1000000000000000000000000000000000000000000000000000(52비트)0011111111111000000000000000000000000000000000000000000000000000
- 부호=
- 만약 32비트를 사용하면 0.5가 어떻게 저장될까?
- 32비트 컴퓨터의 바이어스는 127이고, 부호는 1비트, 지수는 8비트, 맨티사는 23비트를 사용한다.
- 1=
- 유한 정밀도 (finite precision)의 한계
- 가수부가 52비트로 제한되어 있음. 약 15~16자리 10진수까지만 정확히 표현 가능
- 그 이후 자리수는 ‘잘림’(truncation)
- 반올림 오차가(round-off error)가 발생
- 한계 사례
- 0.1 을 저장한다면… 0.1=
0.00011001100110011 ...(무한 반복되어 정확히 저장 불가) - 큰 수와 작은수를 더할 때 \(10^{16}+1-10^{16}=?\)
print(1e16+1-1e16) - 연산 순서에 따라 결과가 달라질 수 있음
# 예제 1: 큰 수 + 작은 수 a = 1e16 # 매우 큰 수 b = 1.0 # 작은 수 c = -1e16 # 큰 음수 res1 = (a + b) + c res2 = a + (b + c) print("(a + b) + c =", res1) print("a + (b + c) =", res2)
- 0.1 을 저장한다면… 0.1=
- ex: 0.80
Week3
- 목표
- 방정식을 해석적(analytic)으로 그리고 수치적(numerical)으로 푸는 방법 비교
- Bisection method 이해하고, 활용할 수 있다.
수업 03-1
-
(방정식을 왜 수치적으로 풀어야 하나), 해석적 풀이 vs. 수치적 풀이, 2차 방정식 손계산
- 해석적 풀이가 가능한 경우
-
1차, 2차 방정식: 공식 존재
$a x^{2} + b x + c = 0 $의 근의 공식
\[x=\frac{-b\pm\sqrt{b^2-4ac}}{2a}\]
-
- 해석적 풀이가 불가능하거나 매우 복잡한 경우
- 5차이상의 다항식의 경우, 근의 공식 없음 (사칙연산이나, 거듭 제곱근 등, 손으로 계산 못한다.) 하지만 실근은 존재한다.
import matplotlib.pyplot as plt import numpy as np def poly(x,*args): """ polynomial function """ n=len(args)-1 y=0. print('n,i,arg') for i, arg in enumerate(args): print(n,i,arg) y+=arg*(x**n) n-=1 return y xs=np.linspace(-1.3,1,100) ys=poly(xs,-5,-2,5,3,2,1) plt.plot(xs,ys,'-')-
\(x=\cos(x)\) 만족하는 \(x\)값 구하기. 근은 분명 존재한다.
import numpy as np import matplotlib.pyplot as plt def func(x): return np.cos(x)-x xs=np.linspace(-10,10) plt.plot(xs,func(xs),label=r'$y=\cos(x)$') plt.axhline(c='k') plt.legend()
- 이분법(bisection method)
- 원리:
- \(f(x)=0\)가 연속일 때, 두 점 \(a,b\)에서 함수값의 부호가 다르면, 그 사이에 반드시 해가 있다. (중간값 정리, Intermediate Value Theorem)
- 즉, [a, b] 구간에서 근이 있음을 알면 구간을 절반으로 줄여가며 해를 찾는 방법
- 원리:
<img src="https://upload.wikimedia.org/wikipedia/commons/c/c2/Bisection_method.png" alt="drawing" width="400"/>
-
알고리듬:
-
시작 구간 \([a,b]\) 선택:
$$f(a)×f(b)<0$$ 위가 반드시 만족되어야 함 (근이 반드시 존재) - 위와 같은 조건 만족하는 $$a,b$$ 값의 중간 값 $$c$$ 구하기. $$c=\frac{a+b}{2}$$ - f(c)의 부호 확인 + case 1. $$f(a)\times f(c)<0$$ 근이 $$[a,c]$$ 안에 존재 + case 2. $$f(c)\times f(b)<0$$ 근이 $$[c,b]$$ 안에 존재 - 새로운 구간을 $$[a,c]$$ 또는 $$[c,b]$$로 좁힘 - 원하는 허용 구간 내 오차가 나올 때 까지 반복. $$E^a \leq Tol. $$ * 예제 방정식 $$x^2=2$$를 풀어보자. + 구간선택: $$[a,b]=[1,2]$$ + 조건 탐색 $$f(1)=-1,f(2)=2$$ 부호가 다르므로, 선택된 구간 $$[1,2]$$ 안에 해 존재. + 중점 설정 $$c=\frac{a+b}{2}=1.5$$ + 조건 탐색 $$f(1.5)=0.25>0$$ + 구간 조정 따라서 근은 $$[1,1.5]$$ 범위 내 존재 - 다시 중점 설정 $$c=\frac{a+b}{2}=1.25$$ + 조건 탐색 $$f(125)=-0.4375<0$$ + 구간 조정 따라서 근은 $$[1.25,1.5]$$사이에 존재 - 중점 빛 범위의 구간 설정을 반복하여 수정하며 오차 좁힘. ```python def f(x): ## f(x)=x^2-2 함수 return x**2 - 2 a=1 b=2 tol=1e-10 error=tol*2 if f(a) * f(b) > 0: print("root not in [a, b]") k=0 while error>tol: #(b - a) / 2 > tol: c = (a + b) / 2 # center if f(a) * f(c) < 0: # opposite sign b = c # update b else: a = c # or update a error=(b-a)/2. k=k+1 print('total iteration:',k) ``` - 내 컴퓨터에서는 33번 반복해야 $$10^{-10}$$ 허용오차 범위내의 근을 구할 수 있었다. - 아래 예시를 통해 upper limit (파란색), lower limit (빨간색)이 반복 횟수에 따라 변하는 과정을 살펴보자. ```python def f(x): ## f(x)=x^2-2 함수 return x**2 - 2 a=1 b=2 tol=1e-2 error=tol*2 if f(a) * f(b) > 0: print("root not in [a, b]") k=0 while error>tol: #(b - a) / 2 > tol: plt.plot(k,a,'ro') plt.plot(k,b,'bo') c = (a + b) / 2 # center plt.plot(k,c,'g+') if f(a) * f(c) < 0: # opposite sign b = c # update b else: a = c # or update a error=(b-a)/2. k=k+1 print('total iteration:',k,'root:',c) print('a,b:',a,b) plt.plot(np.nan,'ro',label='a') plt.plot(np.nan,'bo',label='b') plt.plot(np.nan,'g+',label='center') plt.xlabel('iteration') plt.ylabel('Range') plt.legend() ```
수업 03-2 (Newton-Raphson 1)
-
원리가 쉽고 그리고 근을 찾긴 하지만, 때로는 너무 많은 반복 계산을 필요로 한다. 더욱 빠르고 효율적인 방법이 없을까?
-
아래 그림의 알고리듬을 반복.
-
예제
방정식 \(x^2=2\)를 풀어보자.
- 해석적 해:
-
수치적 해?
알고리듬 (점화식)이 다음과 같다.
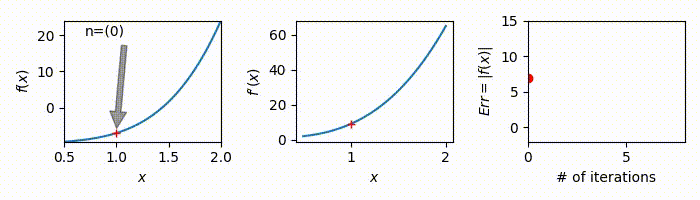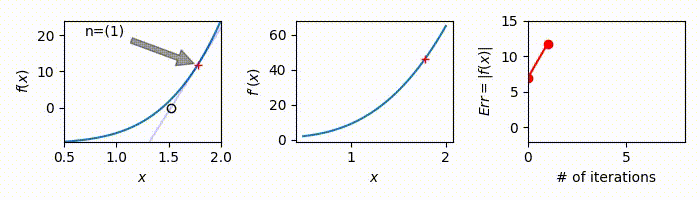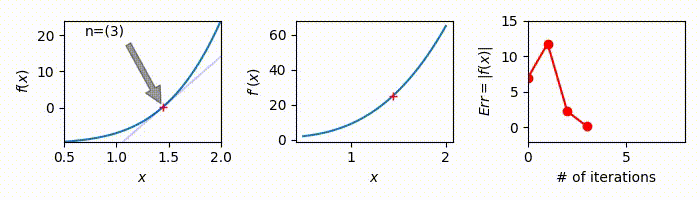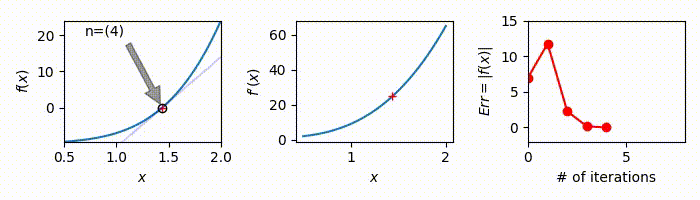
\[x_{n+1}=x_n-\frac{x_n^2-2}{2x_n}\]오차가 항상 있으므로, 허용가능한 오차(tolerance)를 설정해야 하겠다. 절대 오차를 아래와 같이 정의하고, 허용가능한 오차를 \(10^{-10}\)으로 설정하자. \(E^a = |x_{n+1}^2-2|\leq 10^{-10}\)
이 알고리듬은 처음 추측값(\(x_0\))이 필요하다. 이를 \(x_0=+1\)로 설정하고 알고리듬을 적용해보자.
-
At \((n=0)\)
\[x_0=+1\] -
At \(n=1\)
\[x_1=x_0-\frac{x_0^2-2}{2x_0}=1-\frac{1^2-2}{2}=1+0.5=1.5\] \[E^a=|1.5^2-2|=0.25 \ge10^{-10} \therefore \text{not accurate enough}\] -
At \(n=2\)
\[x_2=x_1-\frac{x_1^2-2}{2x_1}=1.5-\frac{1.5^2-2}{3}=1.4166666...\] \[E^a=|1.4166...^2-2|=0.006944...\times 10^{-6}\ge10^{-10} \therefore \text{not accurate enough}\] -
At \(n=3\)
\[x_3=x_2-\frac{x_2^2-2}{2x_2}=1.41421568 ...\] \[E^a=6.007..\times10^{-6}\ge10^{-10} \therefore \text{not accurate enough}\] -
At \(n=4\)
\[x_4=x_3-\frac{x_3^2-2}{2x_3}=1.41421356237...\] \[E^a=4.51\times10^{-12}\red{\lt}10^{-10} \therefore \text{accurate enough!}\]
fig=plt.figure() ax1=fig.add_subplot(121) ax2=fig.add_subplot(122) x=1 ## initial guess ax1.plot(0,x,'o',label='initial guess') tol=1e-10 err=tol*2 k=0 while(err>tol and k< 10): ## k counts the number of iteration. x=x-(x**2-2)/(2*x) err=abs(x**2-2) print(k+1,x,err) print(err<=tol) k=k+1 ## see the trend. ax1.plot(k,x,'+',label=r'$x_%i$'%k) ax2.plot(k,err,'o') #ax2.set_yscale('log') ax1.legend()- Repeat the above with changing the initial guess \(x_0=-1\).
- \(y=x^2-2\) 그래프를 실제로 그리고, 반복할 때 마다 어떻게 값이 변하고 있는지 살펴보자.
-
-
예제
방정식 \(x^2=3\)를 풀어보자.
-
주어진 알고리듬은 아래와 같다.
\[x_{n+1}=x_{n} - \frac{x_n^{2}-3}{2x_{n}}\]
-
-
예제
방정식 \(x^{4}=2\)를 풀어보자.
-
주어진 알고리듬은 아래와 같다.
\[x_{n+1}=x_n-\frac{x_n^4-2}{4x_n^3}\]
-
-
예제
방정식 \(\ln{x}=1\)를 풀어보자.
-
주어진 알고리듬은 아래와 같다.
\[x_{n+1}=x_n-\frac{\ln(x_n)-1}{1/x_n}\]
-
-
예제
방정식 \(\cos{x}=0.3\)를 풀어보자.
-
주어진 알고리듬은 아래와 같다.
\[x_{n+1}=x_n-\frac{\cos(x_n)-0.3}{-\sin(x_n)}\]
-
-
물음: 위 예제에서 보이는 특정 규칙을 찾아보자.
-
물음: 초기값을 바꿔보고 그 영향을 살펴보자.
Week4 (Newton-Raphson 2)
수업 04-1 Taylor series와 Newton-Raphson 법
- 개념
-
아래 형태의 함수의 답을 구하고 싶을 때 사용할 수 있다.
\[f(x)=0\] -
예: \(x^2=2\) 의 해를 구하기 위해서는
\[f(x)=x^2-2=0\]위의 해를 구하면 되겠다.
- Bisection method는 항상 해를 구할 수 있지만, Newton Raphson은 가끔 해를 못구할 때도 (해를 구하는데 실패할 수) 있다.
- 하지만 Bisection method에 비해 훨씬 빠르게 해를 찾을 수 있다.
- ‘접선’을 활용해 해를 빠르게 찾아간다.
- 미지수가 둘 이상은 경우에도 활용가능하다 (Advanced)
- \(f(x,y)=0\) 혹은 \(\boldsymbol f(\boldsymbol v)=0\) 에도 활용 가능.
-
-
Newton Raphson 방법의 도출 1
- 주어진 첫 guess 를 \(x^{(0)}\)라 하자.
-
Newton Raphson 방법의 도출 2
테일러 급수(Taylor series)로부터 Newton Raphson 방법 도출
-
함수 \(f(x)\) 의 테일러 급수에 의하면
\[f(x)=\sum_{n=0}\] \[f(x)=\sum_{n=0}^{\infty}\frac{f^{(n)}(a)}{n!}(x-a)^n =f(a)+f^\prime(a)(x-a)+\frac{1}{2}f^{\prime\prime}(a)(x-a)^2+\frac{1}{6}f^{\prime\prime\prime}(a)(x-a)^3 + ...\] -
Example of \(f(x)=x^2\) 의 경우?
\[f(x)=x^2\] \[f^\prime(x)=2x\] \[f^{\prime\prime}(x)=2\] \[f^{\prime\prime\prime}(x)=0.\]따라서, 이어서 나오는 고차 항의 도함수는 0이 되며 기여하는 바가 없게 된다. 다시 테일러 급수의 정의를 따라,
-
\(a=0\)일 때의 경우(Maclaurin series)를 살펴보면
\[f(x)=f(0)+f^\prime(0)x+\frac{1}{2}f^{\prime\prime}(0)x^2 \newline =0+0\times x+1/2\times 2\times x^2=x^2\] -
\(a=1\)일 때의 경우에는?
\[f(x)=f(1)+f^\prime(1)(x-1)+\frac{1}{2}f^{\prime\prime}(1)(x-1)^2 \newline =1+2(x-1)+(x-1)^2 \newline =1+2x-2+x^2-2x+1=x^2\]
-
-
Newton-Raphson 식 도출 (1st order)
\[f(x)=0\]을 풀이하는 문제가 있다 가정하자. 이때 이를 위 의 \(a\)값을 \(x_n\)라 놓고 풀면
\[f(x)=f(x_n)+f^\prime(x_n)(x-x_n)+\frac{1}{2}f^{\prime\prime}(x_n)(x-x_n)^2+ ...\]여기서 \(n=1\)까지 항만 고려한다면..
\[f(x)\approx f(x_n)+f^\prime(x_n)(x-x_n)\]우리가 풀이하고자 하는 조건에 의하면 \(f(x)=0\) 이므로
\[0\approx f(x_n)+f^\prime(x_n)(x-x_n)\]따라서 \(x\)에 대해 풀이하면
\[-\frac{f(x_n)}{f^\prime(x_n)}\approx x-x_n\]아래가 도출된다.
\[\rightarrow x\approx x_n-\frac{f(x_n)}{f^\prime(x_n)}\]이 때 근사된 \(x\)을 다음번 추측값 \(x_{n+1}\)이라 하면 Newton-Raphson에 활용되는 반복식이 얻어진다.
-
2nd order Newton-Raphson 식
- Taylor 공식에서 2차 오더까지 사용하면 어떠한 Newton-Raphson식이 도출되나?
-
도출
\[f(x)\approx f(x_n)+f^\prime(x_n)(x-x_n)+\frac{1}{2}f^{\prime\prime}(x_n)(x-x_n)^2\]급수의 중심을 바꾸기 위해 \(h\)값을 아래와 같이 도입하자
\[h=x-x_n\]그러면 2차항까지의 테일러 급수가 아래와 같이 표현된다.
\[f(x_n+h)\approx f(x_n)+f^\prime(x_n)h+\frac{1}{2}f^{\prime\prime}(x_n)h^2\]그 다음 좌항이 0이 되면
\[0\approx f(x_n)+f^\prime(x_n)h+\frac{1}{2}f^{\prime\prime}(x_n)h^2\]\(h\)에 대한 2차 방정식이므로, 근의 공식을 사용하면
\[h=\frac{-f^\prime(x_n)\pm\sqrt{[f^\prime(x_n)]^2-2f(x_n)f^{\prime\prime}(x_n)}}{f^{\prime\prime}(x_n)}\]위 계산으로 구해진 \(h\)를 활용해서
\[x_{n+1}=x_{n}+h\] -
주의
근의 공식에 따른 두 \(h\)값 중에 무엇을 선택해야 하나? 대부분의 경우 두 값을 비교하여 더욱 작은 \(h\)값을 활용한다.
-
- 예제
- 방정식 \(x^2+x=10\)을 풀어보자.
-
우선 \(f(x)=0\) 형태로 바꿔 표현하면,
\[f(x)=x^2+x-10=0\]혹은
\[f(x)=-x^2-x+10=0\]이 된다. 사실 어느 쪽을 고르나 동일한 알고리듬이 적용 가능하다. 전자의 경우를 선택하고 파이썬으로 함수 \(f(x)\)를 표현해보자.
def func(x): return x**2+x-10풀이에 의하면 함수의 도함수 \(f^\prime(x)\)도 필요하다. 따라서,
\[f^\prime(x)=\frac{\partial f(x)}{\partial x}=2x+1\]파이썬으로 표현하자면
def fprime(x): return 2*x+1이를 활요해 아래 알고리듬에 대입하면
\[x_{n+1}\leftarrow x_n-\frac{f(x_n)}{f^\prime(x_n)}\]x=1 # initial guess x=x-func(x)/fprime(x)여기에 tolerance를 추가한다면
x=1 # initial guess tol=1e-10 err=abs(func(x)) while err>tol: x=x-func(x)/fprime(x) err=abs(func(x))- 초기값을 바꿔보고 그 영향을 살펴보자.
-
고급 예제: 위 경우를 아래와 같이 2nd order Taylor expansion을 활용해 작성해보자.
\[h=\frac{-f^\prime(x_n)\pm\sqrt{[f^\prime(x_n)]^2-2f(x_n)f^{\prime\prime}(x_n)}}{f^{\prime\prime}(x_n)}\]위 계산으로 구해진 $h$를 활용해서
\[x_{n+1}=x_{n}+h\] -
아래는 Halley’s method으로 알려진 방법이다.
\[x_{n+1}=x_n-\frac{2f(x_n)f^\prime(x_n)}{2[f^\prime(x_n)]^2-f(x_n)f^{\prime\prime}(x_n)}\]이를 활용해
\[f(x)=\cos(x)e^{3x}-3=0\]을 만족하는 \(x\)값을 구하시오.
- 1st and 2nd order Newton-Raphson과 Halley’s method 비교 예제
import matplotlib.pyplot as plt import numpy as np def f(x): return np.cos(x)*np.exp(3*x)-3 def fp(x): return np.cos(x)*np.exp(3*x)*3-np.sin(x)*np.exp(3*x) def fpp(x): return -np.sin(x)*np.exp(3*x)*3+np.cos(x)*np.exp(3*x)*9 def h(x): # 2nd order NR F=f(x) p=fp(x) pp=fpp(x) det=p**2-2*F*pp det=np.sqrt(det) h1=-p+det h1=h1/pp h2=-p-det h2=h2/pp if abs(h1)<abs(h2): return h1 else: return h2 def Halley(x): ## Halley's term F=f(x) p=fp(x) pp=fpp(x) return 2*F*p/(2*p**2-F*pp) xs=np.linspace(-2.5,1) ys=func(xs) fig=plt.figure(figsize=(7,3)) ax1=fig.add_subplot(121) ax2=fig.add_subplot(122) ax1.plot(xs,ys) xinit=-0.1 tol=1e-10 ## Newton Raphson x=xinit err=tol*2 i=0 while err>tol: ax1.plot(x,f(x),'ko',mfc='None') ax2.plot(i,f(x),'ko') x+=-f(x)/fp(x) err=abs(f(x)) i+=1 ## 2nd order x=xinit err=tol*2 i=0 while err>tol: ax1.plot(x,f(x),'r+') ax2.plot(i,f(x),'r+') x+=+h(x) # here it is + sign. err=abs(f(x)) i+=1 ## Halley's method ## 2nd order x=xinit err=tol*2 i=0 while err>tol: print(i,x) ax1.plot(x,f(x),'bx') ax2.plot(i,f(x),'bx') x-=Halley(x) # note the minus sign here! err=abs(f(x)) i+=1
수업 04-2 (2차 방정식 풀이 Python module 만들기)
- 고급 예제: 임의의 2차 함수의 해를 찾는 script를 작성해보자.
- 고급 예제: CLI 환경에서 \(a,b,c\) 를 줬을 때, \(ax^2+bx+c=0\)의 해를 찾는 모듈을 만들어보자.
Week5 (연립 방정식)
수업 05-1 (연립 방정식 소개)
-
2원 연립 방정식
\[\bigg( \begin{matrix} 2x+y=5 \ \ \text{eq. (1)}\\ x-y=-1 \ \ \text{eq. (2)} \end{matrix}\]미지수가 \(x,y\) 두 개 (2원), 식도 2개!
- 대입법 (손으로 풀이)
-
식 (2)를 바꿔서 \(y=x+1\) 이라 정리되고, 이를 다시 식 (1)에 대입하면,
-
식 (1)이
\[2x+(x+1)=5\]로 바뀌고
\[3x=4\rightarrow x=4/3\]따라서
\[y=4/3+1=7/3\] -
주어진 연립방정식을 만족하는 \((x,y)\) 짝을 완성
\[x=4/3, y=7/3\]
-
-
가감법 (덧셈이나 뺄셈을 활용해 손으로 풀이)
-
식 (1)+식(2) 혹은 식 (1) - 식(2) 등을 활용
-
식 (1)과 식(2)를 더하면
\[3x=4\]따라서 \(x\)와 \(y\)를 이어 구할 수 있다.
-
- 대입법 (손으로 풀이)
-
기하학적 의미 2원 1차 연립 방정식에서 각 방정식은 각기 다른 ‘직선’을 의미
\[2x+y=5 \rightarrow y=-2x+5\] \[x-y=-1 \rightarrow y=x+1\]두 직선의 교점 \((x,y)=(3/4,7/3)\)
import matplotlib.pyplot as plt import numpy as np ## the two lines def y1(x): return 5-2*x def y2(x): return x+1 xs=np.linspace(-2,4) ## -10~10 범위 내의 선 그리기 plt.plot(xs,y1(xs),'r-',label='Line 1') plt.plot(xs,y2(xs),'b-',label='Line 2') xy=(4/3,7/3) # actual solution plt.plot(*xy,marker='+',mfc='None',mec='k',ms=10) # deco plt.legend() -
3원 연립 방정식
\[\bigg( \begin{matrix} 2x+y+z=5 \ \ \text{eq. (1)}\\ x-y-z=-1 \ \ \text{eq. (2)}\\ x+5y+2z=0 \ \ \text{eq. (3)} \end{matrix}\]미지수가 \(x,y,z\) 세 개 (3원), 식도 3개!
-
기하학적 의미? 서로 다른 세 면이 만나는 점.
import matplotlib.pyplot as plt import numpy as np %matplotlib widget def z1(x,y): return 5-2*x-y def z2(x,y): return x-y+1 def z3(x,y): return (-x-5*y)/2. nres=10 x=np.linspace(-10,10,nres) y=np.linspace(-10,10,nres) xx,yy=np.meshgrid(x,y) zz1=z1(xx,yy) zz2=z2(xx,yy) zz3=z3(xx,yy) fig=plt.figure() ax1=fig.add_subplot(projection='3d') kws=dict(alpha=0.5) ax1.plot_surface(xx,yy,zz1,color='r',**kws) ax1.plot_surface(xx,yy,zz2,color='g',**kws) ax1.plot_surface(xx,yy,zz3,color='b',**kws) ## actual point xyz=1.3333333,-2, 4.3333333 ax1.scatter(*xyz,color='k',marker='o')
수업 05-2 (행렬을 활용한 풀이)
- 2원 연립 방정식 풀이
-
우선 풀이를 위해서는 연립 방정식을 행렬의 형태로 바꿔야 한다.
\[\bigg( \begin{matrix} 2x+y=5 \ \ \text{eq. (1)}\\ x-y=-1 \ \ \text{eq. (2)} \end{matrix}\]을 다음의 행렬 형태로 바꾸자.
\[\begin{bmatrix} 2& 1\\ 1&-1\\ \end{bmatrix} \begin{bmatrix} x\\ y \end{bmatrix} = \begin{bmatrix} 5\\ -1 \end{bmatrix}\]위처럼 연립 방정식을 행렬의 형태로 바꿔서 풀이할 수 있다. 따라서 연립 방정식을 행렬 형태로 바꾸는 연습이 필요.
- 예시
- 아래 연립 방정식을 행렬의 형태로 바꿔보세요. \(\bigg( \begin{matrix} x-5=y \\ y-3x+3=0 \end{matrix}\)
- 답 \(\begin{bmatrix} 1&-1\\ -3&1\\ \end{bmatrix} \begin{bmatrix} x\\ y \end{bmatrix} = \begin{bmatrix} 5\\ -3 \end{bmatrix}\)
- 아래 연립 방정식을 행렬의 형태로 바꿔보세요. \(\bigg( \begin{matrix} x=y \\ y=3+x \end{matrix}\)
- 답 \(\begin{bmatrix} 1&-1\\ 1&-1\\ \end{bmatrix} \begin{bmatrix} x\\ y \end{bmatrix} = \begin{bmatrix} 0\\ -3 \end{bmatrix}\) ** 하나의 형태로만 답이 나오는 건 아닙니다. 예를 들어 위의 경우 \(\begin{bmatrix} 1&-1\\ -1&1\\ \end{bmatrix} \begin{bmatrix} x\\ y \end{bmatrix} = \begin{bmatrix} 0\\ 3 \end{bmatrix}\) 으로 표기될 수 있습니다. 하지만 형태가 다르더라도 정답은 동일하게 도출됩니다.
** 그리고 위의 경우에는 해가 없습니다!! 왜 그럴까요?
- 아래 연립 방정식을 행렬의 형태로 바꿔보세요. \(\bigg( \begin{matrix} x-5=y \\ y-3x+3=0 \end{matrix}\)
-
해가 없는 경우?
\[\bigg( \begin{matrix} 2x+y=5 \ \ \text{eq. (1)}\\ 2x+y=-1 \ \ \text{eq. (2)} \end{matrix}\]위 연립방정식을 만족하는 해는 없습니다. 왜 그럴까요?
-
행렬을 보고 해가 없는 경우를 ‘판별’할 수 있을까요? 판별(determination)하기 위해 우리는 ‘판별값’ 혹은 ‘판별식’이라고 불리는 determinant를 구해서 알 수 있다.
-
예를 들어, 2x2행렬의 경우
\[\begin{bmatrix} a & b\\ c & d \end{bmatrix}\]의 판별값을 아래와 같이 표기한다.
\[\begin{vmatrix} a & b\\ c & d \end{vmatrix} =ad-bc\] -
3x3행렬의 경우
\[\begin{bmatrix} a & b\\ c & d \end{bmatrix}\]의 판별값을 아래와 같이 표기한다.
\[\begin{vmatrix} a & b & c \\ d&e&f\\ g&h&i \end{vmatrix} =aei+bfg+cdh-ceg-bdi-afh\]
-
- 행렬로 표현된 연립방정식은 여러 ‘규칙성’을 가진 알고리듬을 통해 그 해를 구할 수 있습니다.
- 행렬로 표현된 수식을 풀이하는 방법은 크게 2가지로 나뉠 수 있음.
- 직접해법 (direct method)
- 반복해법 (iterative method)
- Jacobi method
- Gauss-Seidel method
- 반복해법은 발산하는 경우가 더러 있음. 항상 해를 찾을 수 있지 않음. 따라서 수치안정성이 낮음
- 가우스 소거법
- 기본 개념
- 확장행렬(augmented matrix) 만들기
- 두행 (가로줄)의 교환
- 한 행에 0이 아닌 상수를 곱함 (scaling)
- 한행에 다른 행의 배수를 더함 (row addition)
- 2-4을 반복하며 삼각형 모양의 행렬을 만듦
- Diagnolization
- 삼각형 행렬이 다 만들어지면 아래에서부터 거꾸로 대입 (back-substitution)
-
예를 들어 아래 행렬식을 푼다면
\[\begin{bmatrix} 2& 3 & 1 \\ 1& -1 & 1\\ 3& 11 & 5 \end{bmatrix} \begin{bmatrix} x\\ y\\ z \end{bmatrix} = \begin{bmatrix} 9\\ 1\\ 35 \end{bmatrix}\]-
우선 좌변의 3x3행렬과 우변의 3x1’벡터’를 결합한 3x4확장 행렬을 만듭니다.
\[\left[ \begin{array}{ccc|c} 2& 3 & 1 & 9\\ 1& -1 & 1 & 1\\ 3& 11 & 5 & 35 \end{array} \right] \begin{array}{c} \text{1st row}\\ \text{2nd row}\\ \text{3rd row} \end{array} \begin{array}{c} \text{irow=0}\\ \text{irow=1}\\ \text{irow=2} \end{array}\]그리고 이를 행렬 \(\boldsymbol A\)라 부릅시다. 따라서 아래와 같습니다.
\[\begin{bmatrix} A_{11} & A_{12} & A_{13} & A_{14} \\ A_{21} & A_{22} & A_{23} & A_{24} \\ A_{31} & A_{32} & A_{33} & A_{34} \\ \end{bmatrix} = \left[ \begin{array}{ccc|c} 2& 3 & 1 & 9\\ 1& -1 & 1 & 1\\ 3& 11 & 5 & 35 \end{array} \right]\]파이썬을 활용해 구현한다면 아래와 같습니다.
def show(A,fmt='%+7.2f'): """ Function to more neatly print out the matrix. """ print('--') for i, As in enumerate(A): cr='' for j, a in enumerate(As): cr=f'{cr} {fmt}'%a print(cr) import numpy as np A=np.zeros((3,4)) # 3 x 4 (three rows, four columns) (3행, 4열) A[0,:]=2, 3, 1, 9 #irow=0 A[1,:]=1,-1, 1, 1 #irow=1 A[2,:]=3,11, 5,35 #irow=2 show(A) ## 말끔하게 행렬을 소수 2째자리 까지만 출력해서 봅시다.위에서 함수
show는 행렬을 말끔하게 출력하기 위해서 간략히 작성해 봤습니다. - 행의 위치를 교환합니다 (optional입니다. 하지만 truncation 오차를 줄여줍니다).
- 첫번째 열(즉
A[:,0])의 절대값이 높은 순서대로 아래에서부터 위로 채웁니다. - 1열 즉
을 따라서, 3번째 행(3rd row)의 1열(1st col.) 값, 즉 \(A_{13}\)의 절대 값
\[|A_{13}|=\green{3}\]이며 가장 큰 수입니다. 그 다음이 \(|A_{11}|=\blue{2}, A_{12}=\red{1}\) 순서입니다.
\[\left[ \begin{array}{ccc|c} \red{1}& \red{-1} & \red{1} & \red{1}\\ \blue{2}& \blue{3} & \blue{1} & \blue{9}\\ \green{3}& \green{11} & \green{5} & \green{35} \end{array} \right] \begin{array}{c} \text{2nd row}\rightarrow\text{3rd row}\\ \text{1st row}\rightarrow\text{2nd row}\\ \text{3rd row}\rightarrow\text{1st row} \end{array}\]행렬 옆에 표기된 방법대로 row를 바꾸면
\[\left[ \begin{array}{ccc|c} \green{3}& \green{11} & \green{5} & \green{35} \\ \blue{2}& \blue{3} & \blue{1} & \blue{9}\\ \red{1}& \red{-1} & \red{1} & \red{1} \end{array} \right]\]위 순서 까지를 Python 코드로 옮기면
#------------------------------------------------ import numpy as np # initial empty A. A=np.zeros((3,4)) # filling up the matrix. A[0,:]=2, 3, 1, 9 #1st row, irow=0 A[1,:]=1,-1, 1, 1 #2nd row, irow=1 A[2,:]=3,11, 5,35 #3rd row, irow=2 show(A) B=A.copy() ## copy to a temp matrix, and named it `B` A[::]=0. ## zeroed. A[0,:] = B[2,:] # 3rd row [3,11,5,35] -> 1st row A[1,:] = B[0,:] # 1st row [2, 3, 1,9] -> 2nd row A[2,:] = B[1,:] # 2nd row [1,-1, 1,1] -> 3rd row show(A)그런데, \(A\) 행렬의 순서를 바꾸는 걸 Python에게 시키고 싶다면 np.argsort를 다음과 같이 활용할 수 있겠다.
print(A[:,0]) #1열 - 혹은 A[0:3,0] # 위 결과는 [2,1,3] 순서가 된다. 그런데 우리는 절대 값의 순서가 필요. # 따라서 np.abs 을 활용해 절대값을 print(np.abs(A[:,0])) # 1열을 따라 낮은 값에서 순서대로 인덱스를 저장. ind = np.argsort(np.abs(A[:,0])) # show(A[ind,:]) #낮은->높은 값 순서대로 바뀜. show(A[ind[::-1],:]) #높은->낮은 값 순서대로... ind[::-1] - 첫번째 열(즉
- 전진 소거 (forward elimination)
- 앞서 재 정렬된 행렬은 아래와 같다.
- 첫번째 행의 첫번째 렬 값,
A[0,0], 즉 \(\green{3}\)을 분자로 그리고 \(\blue{\text{row2}}\), 첫번째 렬(col1) 값, 즉 \(A_{21}\),A[1,0]\(=\blue{2}\)을 분모로 하는 factor \(\frac{\green{3}}{\blue{2}}\)을 두번째 행,A[1,:]에 곱해서 첫번째 행에서 뺀 후, 두번째 행을 대체합니다. Python으로 정리하면 아래와 같습니다.
# irow=1 A[1,:]=A[0,:]-(A[0,0]/A[1,0])*A[1,:]- 위 작업을 3번째 행에도 동일하게 수행하면
# irow=2 A[2,:]=A[0,:]-(A[0,0]/A[2,0])*A[2,:]- 그런데 이를 한번에 loop안에 적용할 수 있습니다. 즉:
#------------------------------------------------ import numpy as np # initial empty A. A=np.zeros((3,4)) # filling up the matrix. A[0,:]=2, 3, 1, 9 #1st row, irow=0 A[1,:]=1,-1, 1, 1 #2nd row, irow=1 A[2,:]=3,11, 5,35 #3rd row, irow=2 show(A) B=A.copy() ## copy to a temp matrix, and named it `B` A[::]=0. ## zeroed. A[0,:] = B[2,:] # 3rd row [3,11,5,35] -> 1st row A[1,:] = B[0,:] # 1st row [2, 3, 1,9] -> 2nd row A[2,:] = B[1,:] # 2nd row [1,-1, 1,1] -> 3rd row show(A) for irow in range(1,3): A[irow,:]=A[0,:]-(A[0,0]/A[irow,0])*A[irow,:] show(A) - 다시 행교환
- 이제 행렬은 아래와 같은 형태가 됩니다.
이제 우리의 기준은 \(A_{22}\) 즉
\[\boldsymbol A= \left[ \begin{array}{ccc|c} \green{3}& \green{11} & \green{5} & \green{35} \\ \red{0}& \red{14} & \red{2} & \red{32} \\ \blue{0}& \blue{6.5} & \blue{3.5} & \blue{21.5} \end{array} \right]\]A[1,1]입니다. 그런데 \(|\blue{6.5}|<|\red{14}|\) 이므로 행 교환이 필요합니다.# swap ind = np.argsort(np.abs(A[1:,1])) A[1:,]=A[1:,][ind[::-1],:] show(A) - 다시 전진소거
-
전진 소거의 기준이, 앞서 살펴보았듯 \(A_{22}\)부터 입니다. 즉,
\[\blue{A_{3,:}}\leftarrow\red{A_{2,:}}-A_{22}/A_{32}\times \blue{A_{3,:}}\]icol=1 # A{:,2} irow=2 # A{3,:} A[irow,:]=A[icol,:]-(A[icol,icol]/A[irow,icol])*A[irow,:] show(A)즉 앞서 이어온 결과와 다 모아 행바꾸기, 전진 소거를 표현하자면 아래와 같다.
#------------------------------------------------ import numpy as np # initial empty A. A=np.zeros((3,4)) # filling up the matrix. A[0,:]=2, 3, 1, 9 #1st row, irow=0 A[1,:]=1,-1, 1, 1 #2nd row, irow=1 A[2,:]=3,11, 5,35 #3rd row, irow=2 show(A) # swap icol=0 ind = np.argsort(np.abs(A[icol:,icol])) A=A[ind[::-1],:] show(A) # forward for irow in range(icol+1,A.shape[0]): A[irow,:]=A[icol,:]-(A[icol,icol]/A[irow,icol])*A[irow,:] show(A) # swap icol=1 ind = np.argsort(np.abs(A[icol:,icol])) A[icol:,]=A[icol:,][ind[::-1],:] show(A) # forward for irow in range(icol+1,A.shape[0]): A[irow,:]=A[icol,:]-(A[icol,icol]/A[irow,icol])*A[irow,:] show(A)여기서 icol=0,1로 바뀌며 동일한 코드가 반복되는 걸 알 수 있다.
-
- Swap/Forward 축약 표기
- 앞 단계의 결과를 행렬의 크기와 swap/forward의 대상 행과 열을 고려하여 더욱 축약하자면 아래와 같이 표현된다.
A=np.zeros((3,4)) # filling up the matrix. A[0,:]=2,3,1,9 A[1,:]=1,-1,1,1 A[2,:]=3,11,5,35 for icol in range(0,A.shape[0]-1): ## swap a=np.abs(A[icol:,icol]) ## Based on [absolute values] of a portion of column ind=np.argsort(a) ind=ind[::-1] # reverse order A[icol:,:]=A[icol:,:][ind,:] show(A) ## forward for irow in range(icol+1,A.shape[0]): A[irow,:]=A[irow,:]-A[irow,icol]/A[icol,icol]*A[icol,:] show(A) print('****************')- 그 결과는 아래와 같다
- Diagnalization
- 앞선 단계의 결과를 더욱 진행하여 대각선 값들을 제외하고
0을 만들 수 있다. 아래 코드를 참고하자.
# now one could 'diagonalize' for icol in range(A.shape[0]-1,0,-1): for irow in range(0,icol): f=A[irow,icol]/A[icol,icol] A[irow,:]=A[irow,:]-f*A[icol,:]그 결과는 아래와 같다.
\[\left[ \begin{array}{ccc|c} +3.00& -0.00& +0.00& +1.00 \\ +0.00& -4.67& +0.00& -8.94 \\ +0.00& +0.00& -1.71& -4.43 \end{array} \right]\]정리하자면, 현재 연립 방정식은 아래와 같은 형태가 된 것이다.
\[\left[ \begin{array}{c} +3.00x=+1.00 \\ -4.67y=-8.94 \\ -1.71z=-4.43 \end{array} \right]\]각 식을 풀기 위해서는 행렬의 대각선 값들을 각 행에 각가 나눠주면 되겠다. 즉 아래와 같은 수행을 하고 나면
\[\left[ \begin{array}{ccc|c} +1.00& -0.00& +0.00& +0.33 \\ -0.00& +1.00& -0.00& +1.92 \\ -0.00& -0.00& +1.00& +2.58 \end{array} \right]\]for icol in range(A.shape[0]): A[icol,:]=A[icol,:]/A[icol,icol]가 되어 \((x,y,z)=(0.33,1.92,2.58)\) 해를 찾게 되었다.
- 앞선 단계의 결과를 더욱 진행하여 대각선 값들을 제외하고
- 전체 코드
- 1-7 단계에 이르는 전체 코드를 살펴보자.
- python code
def show(A,fmt='%+7.2f'): """ Function to more neatly print out the matrix. """ print('--') for i, As in enumerate(A): cr='' for j, a in enumerate(As): cr=f'{cr} {fmt}'%a print(cr) import numpy as np # initial empty A. A=np.zeros((3,4)) # filling up the matrix. A[0,:]=2,3,1,9 A[1,:]=1,-1,1,1 A[2,:]=3,11,5,35 #show(A) # swap and forward for icol in range(0,A.shape[0]-1): ## swap a=np.abs(A[icol:,icol]) ind=np.argsort(a) ind=ind[::-1] # reverse order A[icol:,:]=A[icol:,:][ind,:] ## forward for irow in range(icol+1,A.shape[0]): A[irow,:]=A[irow,:]-A[irow,icol]/A[icol,icol]*A[icol,:] show(A) # now one could 'diagonalize' for icol in range(A.shape[0]-1,0,-1): for irow in range(0,icol): f=A[irow,icol]/A[icol,icol] A[irow,:]=A[irow,:]-f*A[icol,:] show(A) for icol in range(A.shape[0]): A[icol,:]=A[icol,:]/A[icol,icol] show(A)** 덧붙이는 말: 중간에 row의 순서를 바꾸는 과정이 없는 알고리듬으로 구현한 웹 프로그램을 여기에서 찾을 수 있습니다.
-
- 기본 개념
- 가우스소거법 예제.
-
위 코드를 활용해 아래를 풀어보자.
\[\left[ \begin{array}{cccc|c} +2 & +3 & +1 & +9 & -1 \\ -1 & -1 & -1 & +1 & +10 \\ +3 & +3 & -5 & +35 & +0 \\ +3 & +4 & +10 & +3 & -3 \end{array} \right]\]
-
-
Numpy의 선형대수(Linear Algebra) 패키지 (np.linalg) 활용
import numpy A=np.zeros((3,4)) # filling up the matrix. A[0,:]=2,3,1,9 A[1,:]=1,-1,1,1 A[2,:]=3,11,5,35 n=A.shape[0] ## determinant 를 구한다. print('det:',np.linalg.det(A[:,:n])) # Inverse matrix 구한 다음 곱하기. root=np.linalg.inv(A[:,:n])@A[:,n] print(root) # 혹은 solve를 활용해서 print(np.linalg.solve(A[:,:n], A[:,n]))
- 행렬로 표현된 수식을 풀이하는 방법은 크게 2가지로 나뉠 수 있음.
-
Week6
수업 06-1
- LU decomposition
- Gauss 소거법과 더불어 설명되는 연립 방정식 풀이법
-
개념 \(\boldsymbol A\cdot \boldsymbol x = \boldsymbol b\)
를 만족시키는 벡터 \(\boldsymbol x\)의 \(x_1,x_2,...,x_n\)을 구하는 방법 중에 하나로써, 행렬 \(\boldsymbol A\)를 아래와 같이 나뉘어 활용한다.
\[\boldsymbol A=\boldsymbol L \cdot \boldsymbol U\]\(\boldsymbol L\): Lower triangular matrix (대각선을 따라서 1)
\(\boldsymbol U\): Uower triangular matrix
4x4행렬을 예로 들자면
\[\boldsymbol A = \begin{bmatrix} A_{11} & A_{12} & A_{13} & A_{14}\\ A_{21} & A_{22} & A_{23} & A_{24}\\ A_{31} & A_{32} & A_{33} & A_{34} \\ A_{41} & A_{42} & A_{43} & A_{44} \end{bmatrix} = \begin{bmatrix} 1 & 0 & 0 & 0\\ L_{21} & 1 & 0 &0 \\ L_{31} & L_{32} & 1 &0 \\ L_{41} & L_{42} & L_{43} &1 \\ \end{bmatrix} \cdot \begin{bmatrix} U_{11} & U_{12} & U_{13} & U_{14}\\ 0 & U_{22} & U_{23} & U_{24} \\ 0 & 0 & U_{33} & U_{34} \\ 0 & 0 & 0 & U_{44} \\ \end{bmatrix}\] -
예시
\[\boldsymbol A = \begin{bmatrix} 2& 1& 0 & 3 \\ 4& 4& 1& 7 \\ 2 &-1& 2 &4 \\ 6 & 7 & 5& 15 \end{bmatrix} = \begin{bmatrix} 1 & 0 & 0 & 0\\ L_{21} & 1 & 0&0 \\ L_{31} & L_{32} & 1 &0 \\ L_{41} & L_{42} & L_{43} & 1 \end{bmatrix} \cdot \begin{bmatrix} U_{11} & U_{12} & U_{13} & U_{14}\\ 0 & U_{22} & U_{23} & U_{24}\\ 0 & 0 & U_{33} & U_{34} \\ 0 & 0 & 0 & U_{44} \end{bmatrix}\]
- Jacobi 법
- Newton-Raphson 처럼 반복하여 행렬 풀이
-
개념
\[\boldsymbol A \cdot \boldsymbol x = \boldsymbol b\]\(\boldsymbol A\)가 \(n\times n\)행렬이라 하면, 각 행 \(i\)마다 아래 식이
\[\sum_{j=1}^nA_{ij}x_j=b_i\]만족해야 함. 위 식을 바꿔 표현하여 각 행 \(i\)에 대해 아래와 같이 전개 가능함.
\[A_{ii}x_i+\sum_{j\ne i}^nA_{ij}x_j=b_i\]만약 \(A_{ii}\ne 0\)이면, 고정되어 있는 한 행 $i$에 대한 위 식을 바꿔 \(x_i\)에 대해 표현하면
\[x_i=\frac{1}{A_{ii}}\bigg(b_i-\sum_{j\ne i}^nA_{ij}x_j\bigg)\] -
반복 알고리듬 앞선 식에서 우변과 좌변의 \(\boldsymbol x\)벡터를 각각 직전\((k)\), 그리고 직후 \((k+1)\) 값으로 표현하면
\[x_i^{(k+1)}=\frac{1}{A_{ii}}\bigg(b_i-\sum_{j\ne i}^nA_{ij}x_j^{(k)}\bigg)\]로 표현되며, 위 반복문을 활용해 \(\boldsymbol x\)를 평가함.
-
예시: 2x2
\[\bigg( \begin{matrix} 4x_1+x_2=7 \ \ \text{eq. (1)}\\ x_1+3x_2=8 \ \ \text{eq. (2)} \end{matrix}\]이라면 각 \(i=1,2\) 마다 아래 두 식이 성립된다.
\[x_1^{(k+1)}=\frac{1}{A_{11}}(b_1-\sum_{j\ne 1}A_{1j}x_j^{(k)})=\frac{1}{4}(7-\sum_{j\ne1}A_{1j}x_j^{(k)}) \ \ \ \ Eq. (1) \newline x_2^{(k+1)}=\frac{1}{A_{22}}(b_2-\sum_{j\ne 2}A_{2j}x_j^{(k)})=\frac{1}{3}(8-\sum_{j\ne2}A_{2j}x_{j}^{(k)}) \ \ \ \ Eq. (2)\]초기값 \(\boldsymbol x^{(0)}=(0,0)\)으로 시작해보자.
- Iteration 1
-
식1
\[x_1^{(1)}=\frac{1}{4}(7-\sum_{j\ne 1}A_{1j}x_j^{(0)})=\frac{1}{4}\times 7=1.75\] -
식2
\[x_2^{(k+1)}=\frac{1}{3}(8-\sum_{j\ne 2}A_{2j}x_j^{(k)})=\frac{1}{3}\times8\approx2.667\]
-
- Iteration 2
-
식1
\[x_1^{(2)}=\frac{1}{4}(7-\sum_{j\ne 1}A_{1j}x_j^{(1)})=\frac{1}{4}(7-2.667)=1.083\] -
식2
\[x_2^{(2)}=\frac{1}{3}(8-\sum_{j\ne 2}A_{2j}x_j^{(2)})=\frac{1}{3}(8-1.75)=2.083\]
-
- … 반복
- Iteration 1
- 종료 조건: 오차의 수렴
-
오차 조건 1.
\[|\boldsymbol{A}\cdot\boldsymbol{x}^{(k+1)}-\boldsymbol{b}|<Tol.\] -
오차 조건 2.
\[|\boldsymbol{x}^{(k+1)}-\boldsymbol{x}^{(k)}| < Tol.\]
-
-
예시: 3x3
import matplotlib.pyplot as plt import numpy as np A=np.zeros((3,3)) b=np.zeros(3) # filling up the matrix. A[0,:]=12,3,1 A[1,:]=9,-11,5 A[2,:]=1,-10,-20 b[:]=3,4,5 ndim=b.shape[0] x=np.zeros(ndim) tol=1e-4 err=tol*2 k=0 hist=[] while err> tol and k<100: # max iter. set to 100 newx=np.zeros(ndim) for icol in range(ndim): summation=0. for jrow in range(ndim): if icol==jrow: pass else: summation+=A[icol,jrow]*x[jrow] newx[icol]=(b[icol]-summation)/A[icol,icol] #x[icol]=1/A[icol,icol]*(b[icol]-) err=np.sqrt(((newx-x)**2).sum()) Ea=np.sqrt(((A@newx-b)**2).sum()) x[::]=newx[::] hist.append([err,Ea]) k+=1 hist=np.array(hist) plt.plot(hist[:,0],'-x',label=r'$|\boldsymbol{A}\cdot\boldsymbol{x}^{(k+1)}-\boldsymbol{b}|$') plt.plot(hist[:,1],'-o',label=r'$|\boldsymbol{x}^{(k+1)}-\boldsymbol{x}^{(k)}|$') plt.legend()
Week7 (중간고사)
- 중간고사 운영 지침
- 개인 노트북 지참하여 시험 (인터넷 연결 x)
- chatGPT등 사용하여 cheating시에 F
수업 07-1
수업 07-2
Week8 (multivariate Newton-Raphson method)
수업 08-1 (Build your own multivariate NR function 1)
- 세상 모든 문제들이 선형적(linear)이다면 가우스 소거법을 활용해 풀이가 가능하니 참 좋겠지만, 그렇지 않다… 실은 대부분 흥미로운 일들은 비선형적이다.
-
예를 들어 다음 연립 방정식을 보자.
\[x^2+y^2=7 \newline e^x+y=8\]이 두 식을 만족하는 \((x,y)\)좌표가 존재하는 것은 아래 Python 프로그램을 통해 쉽게 확인할 수 있다.
%matplotlib inline import numpy as np import matplotlib.pyplot as plt ## 1st line ths=np.linspace(-np.pi,np.pi) r=np.sqrt(7) x=np.cos(ths)*r y=np.sin(ths)*r plt.plot(x,y,label='Line1') ## 2nd line x=np.linspace(-3,3) y=8-np.exp(x) plt.plot(x,y,label='Line2') plt.legend() - 두선의 교점을 찾는 방법으로 multivariate Newton-Raphson method를 활용할 수 있다.
- Single variate Newton-Raphson method는 이미 다루었다.
-
아래 알고리듬을 따르면 되었다.
\[x^{(n+1)}=x^{(n)}-\frac{f(x^{(n)})}{f^\prime(x^{(n)})}\] - Multivariate Newton-Raphson method의 알고리듬도 유사한 형태이다.
-
우선 앞서 다루었던 연립방정식을 아래와 같이 표현하자.
\[f_1(x_1,x_2)=x_1^2+x_2^2-7 \newline f_2(x_1,x_2)=e^{x_1}+x_2-8\]def func(x1,x2): f=np.zeros(2) # f[0]=x1**2+x2**2-7 f[1]=np.exp(x1)+x2-8 return f -
그런 다음 Jacobian matrix를 구하자. 이는 아래와 같이 정의된다.
\[J_{ij}=\frac{\partial f_i}{\partial x_j}\]따라서,
\[J_{11}=\frac{\partial f_1}{\partial x_1}=2x_1 \newline J_{12}=\frac{\partial f_1}{\partial x_2}=2x_2 \newline J_{21}=\frac{\partial f_2}{\partial x_1}=e^{x_1} \newline J_{22}=\frac{\partial f_2}{\partial x_2}=1\]def jacob(x1,x2): j=np.zeros(2,2) # 2x2 jacob j[0,0]=2*x1 j[0,1]=2*x2 j[1,0]=np.exp(x1) j[1,1]=1 return j -
그런 다음 아래 알고리듬을 따르면 된다.
\[x^{n+1}_1=x^{n}_1-J_{11}^{-1}f_1(x^n_1,x^n_2)-J_{12}^{-1}f_2(x^n_1,x^n_2) \newline x^{n+1}_2=x^{n}_2-J_{21}^{-1}f_1(x^n_1,x^n_2)-J_{22}^{-1}f_2(x^n_1,x^n_2)\]위 식을 행렬식을 활용해 표현하자면 아래와 같다.
\[\begin{bmatrix} x_1^{n+1}\\ x_2^{n+1} \end{bmatrix} = \begin{bmatrix} x_1^{n}\\ x_2^{n} \end{bmatrix} - \begin{bmatrix} J_{11}(x_1^n,x_2^n) & J_{12}(x_1^n,x_2^n) \\ J_{21}(x_1^n,x_2^n) & J_{22}(x_1^n,x_2^n) \\ \end{bmatrix}^{-1} \cdot \begin{bmatrix} f_1(x_1^n,x_2^n)\\ f_2(x_1^n,x_2^n) \end{bmatrix}\]아래와 같이 좀 더 간략히 아래와 같이 표기해보자.
\[\begin{bmatrix} \boldsymbol x^{n+1} \end{bmatrix} = \begin{bmatrix} \boldsymbol x^{n} \end{bmatrix} - \begin{bmatrix} \boldsymbol J \end{bmatrix}^{-1} \cdot \begin{bmatrix} \boldsymbol f \end{bmatrix}\]행렬과 벡터를 재배치 해보면…
\[\begin{bmatrix} \boldsymbol J \end{bmatrix} \cdot \begin{pmatrix} \begin{bmatrix} \boldsymbol x^{n+1} \end{bmatrix} - \begin{bmatrix} \boldsymbol x^{n} \end{bmatrix} \end{pmatrix} = \begin{bmatrix} \boldsymbol f \end{bmatrix}\]벡터의 변화량 \(\Delta \boldsymbol x\)를 활용하면
\[\begin{bmatrix} \boldsymbol J \end{bmatrix} \cdot \begin{bmatrix} \Delta \boldsymbol x \end{bmatrix} = -\begin{bmatrix} \boldsymbol f \end{bmatrix}\]로 표현 가능하다. 따라서, 앞서 배운 Gauss 소거법 등을 통해, 역행렬을 계산하지 않고, \([\Delta \boldsymbol x]\)를 구할 수 있다. 그렇게 하기 위해서 아래 정의된
guass함수를 활용하자.def gauss(A): """ Gauss elimination Arguments -------- A: augmented matrix in [n,n+1] dimension Returns ------- Root in [n]-dimensional vector. """ # swap and forward for icol in range(0,A.shape[0]-1): ## swap a=np.abs(A[icol:,icol]) ind=np.argsort(a) ind=ind[::-1] # reverse order A[icol:,:]=A[icol:,:][ind,:] ## forward for irow in range(icol+1,A.shape[0]): A[irow,:]=A[irow,:]-A[irow,icol]/A[icol,icol]*A[icol,:] # now one could 'diagonalize' for icol in range(A.shape[0]-1,0,-1): for irow in range(0,icol): f=A[irow,icol]/A[icol,icol] A[irow,:]=A[irow,:]-f*A[icol,:] for icol in range(A.shape[0]): A[icol,:]=A[icol,:]/A[icol,icol] return A[:,-1]위
gauss함수를 활용해 풀이한 예시이다.## Canvas ## 1st line ths=np.linspace(-np.pi,np.pi) r=np.sqrt(7) x=np.cos(ths)*r y=np.sin(ths)*r ## 2nd line x=np.linspace(-3,3) y=8-np.exp(x) ## Function and Jacobian required for NR procedure def func(x1,x2): f=np.zeros(2) # f[0]=x1**2+x2**2-7 f[1]=np.exp(x1)+x2-8 return f def jacob(x1,x2): j=np.zeros((2,2)) # 2x2 jacob j[0,0]=2*x1 j[0,1]=2*x2 j[1,0]=np.exp(x1) j[1,1]=1 return j ## NEWTON-RAPHSON begins here. # hist arrays for recording changes. ## Initial guess x=np.zeros(2) ## initial guess x[::]=-1.0 ## initial guess # Tolerance setting tol=1e-9 err=tol*2 # n=0 while err>tol and n<50: # jacobian and functions J=jacob(*x) F=func(*x) # Create augmented matrix A A=np.zeros((J.shape[0],J.shape[0]+1)) A[:2,:2]=J[:,:] A[:,-1]=-F[::] # Obtain Delta x via guass elimination method dx=gauss(A) # Update x x=x+dx n+=1 # estimate the error err=np.sqrt((F**2).sum()) print('solution:',x)
-
- Multivariate NR method를 함수화시키자.
def mvNR(func,func_jac,xinit): """ Arguments --------- func: objective function func_jac: jacobian xinit: initial guess on x vectors. Returns ------- x : solution vector hist : trajectory of x vector fhist : trajectory of f vector """ x=xinit[::] # hist arrays for recording changes. hist=[] fhist=[] # Tolerance setting tol=1e-9 err=tol*2 n=0 maxiter=50 while err>tol and n<maxiter: # jacobian and functions J=jacob(*x) F=func(*x) # history hist.append(x) fhist.append(F) # Create augmented matrix A A=np.zeros((J.shape[0],J.shape[0]+1)) A[:2,:2]=J[:,:] A[:,-1]=-F[::] # Obtain Delta x via guass elimination method dx=gauss(A) # updates x, count (n), and error x=x+dx n+=1 err=np.sqrt((F**2).sum()) hist=np.array(hist) fhist=np.array(fhist) return x,hist,fhist -
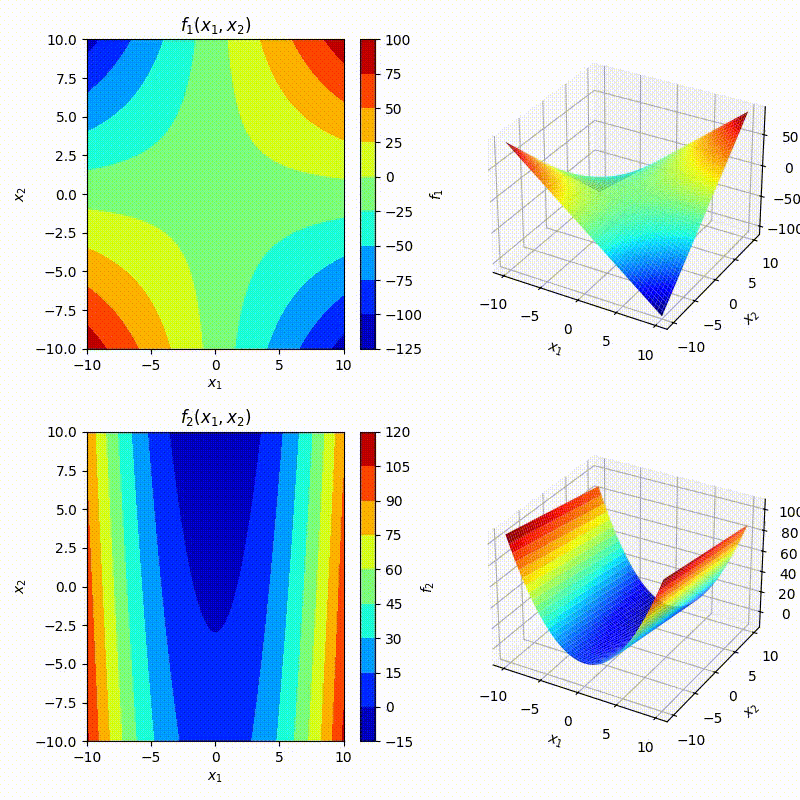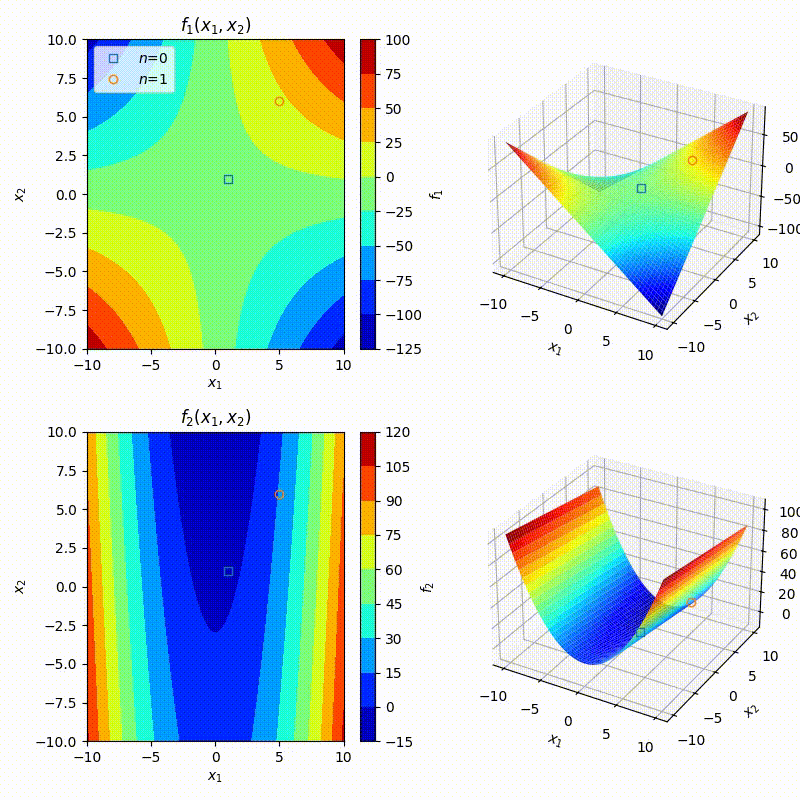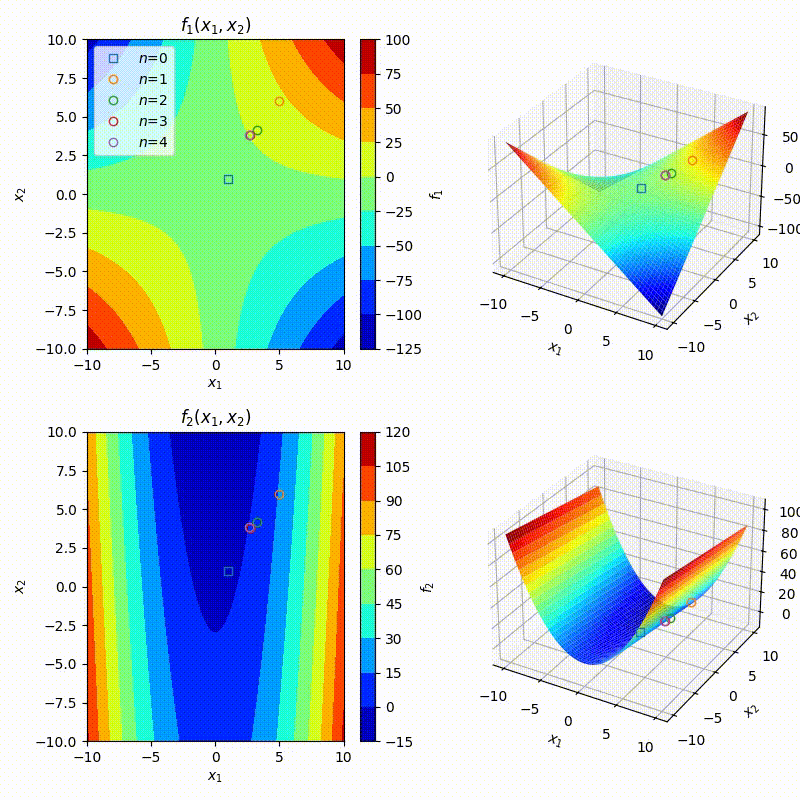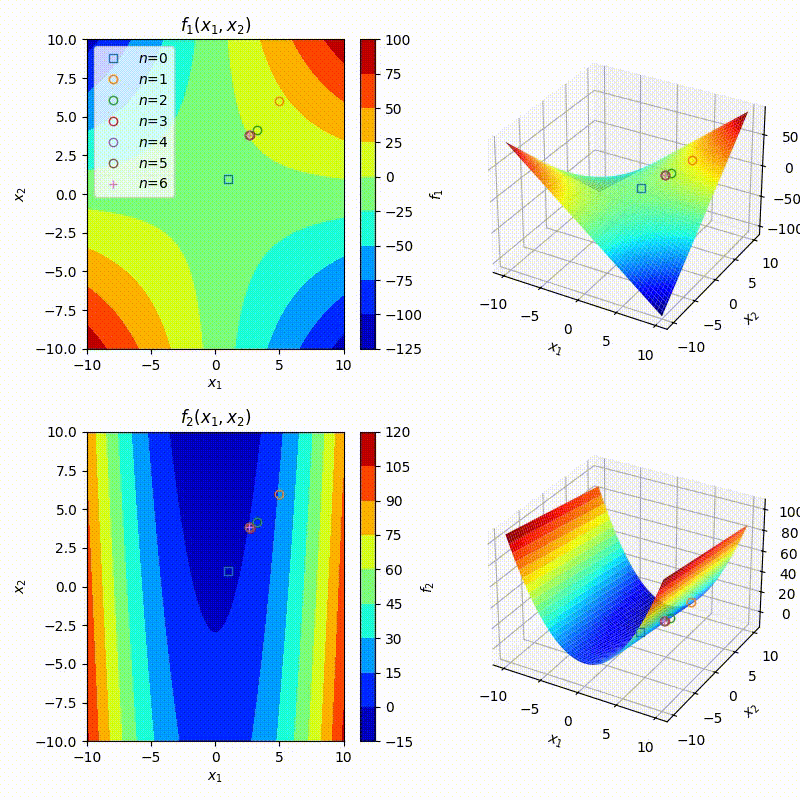
mvNR함수를 앞선guass함수와 함께 사용한다면 아래와 같이 매우 짧은 몇 줄의 코드로 앞선 예제를 작성할 수 있다. 따라서 한번 작성해 놓은 함수를 다시 사용할 수 있게 되었다. 학생들이 이 경험을 통해 모듈화의 이점을 몸소 체험해 보길 바란다.def f1(x,y): return x*y-10 def f2(x,y): return x**2-y-3 def func(x,y): return np.array([f1(x,y),f2(x,y)]) def jacob(x,y): j=np.zeros((2,2)) j[0,0]=y j[0,1]=x j[1,0]=2*x j[1,1]=-1 return j ## NEWTON-RAPHSON begins here. ## Initial guess x=np.zeros(2) ## initial guess x[::]=4.0 ## initial guess x,hist,fhist=mvNR(func,jacob,xinit=np.ones(2))
수업 08-2 (Geomtric interpretation of multivariate NR)
- 앞선 예제를 기하학적으로 해석하자.
-
우선 정형화된 아래 2D 그래프 생선 함수를 사용하자.
def init_fig(f1,f2): fig=plt.figure(figsize=(8,8)) ax1=fig.add_subplot(221)#,projection='3d') ax2=fig.add_subplot(222,projection='3d') ax3=fig.add_subplot(223)#,projection='3d') ax4=fig.add_subplot(224,projection='3d') # Grid x=np.linspace(-10,10,100) y=np.linspace(-10,10,100) X,Y=np.meshgrid(x,y) ## 2D contour plot mappable=ax1.contourf(X,Y,f1(X,Y),cmap='jet') plt.colorbar(mappable,ax=ax1,label=r'$f_1$') ax1.set_title(r'$f_1(x_1,x_2)$') ax1.set_xlabel(r'$x_1$') ax1.set_ylabel(r'$x_2$') ## 3D plane ax2.plot_surface(X,Y,f1(X,Y),cmap='jet') ax2.set_zlabel(r'$f_1$') ax2.set_xlabel(r'$x_1$') ax2.set_ylabel(r'$x_2$') ## 2D contour plot mappable=ax3.contourf(X,Y,f2(X,Y),cmap='jet') plt.colorbar(mappable,ax=ax3,label=r'$f_2$') ax3.set_title(r'$f_2(x_1,x_2)$') ax3.set_xlabel(r'$x_1$') ax3.set_ylabel(r'$x_2$') ## 3D plane ax4.plot_surface(X,Y,f2(X,Y),cmap='jet') ax4.set_zlabel(r'$f_2$') ax4.set_xlabel(r'$x_1$') ax4.set_ylabel(r'$x_2$') return fig,ax1,ax2,ax3,ax4 - 아래 예제를 활용해보자
def f1(x,y): return x*y-10 def f2(x,y): return x**2-y-3 def func(x,y): return np.array([f1(x,y),f2(x,y)]) def jacob(x,y): j=np.zeros((2,2)) j[0,0]=y j[0,1]=x j[1,0]=2*x j[1,1]=-1 return j ## NEWTON-RAPHSON begins here. ## Initial guess x=np.zeros(2) ## initial guess x[::]=4.0 ## initial guess x,hist,fhist,jhist,niters=mvNR(func,jacob,xinit=np.ones(2)) print(f'niters: {niters}') ## Below is to create figures %matplotlib widget #%matplotlib inline fig,ax1,ax2,ax3,ax4=init_fig(f1,f2) kws=dict(mfc='None',zorder=100,ls='None') for n,x in enumerate(hist): f1,f2=fhist[n] x1,x2=x kws.update(label=r'$n$=%i'%n) ax1.plot(x1,x2,**kws) ax2.plot(x1,x2,f1,**kws) ax3.plot(x1,x2,**kws) ax4.plot(x1,x2,f2,**kws) ax1.legend(loc='upper left') - 아래 그림을 보고 어떠한 일이 일어나고 있는지 이해해보자.