데이터 재료과학

데이터 분석/해석 및 시각화(그래프) 등 기초 컴퓨터 활용 능력

Orientation

수업 소개

In the order of preference:

세부 수업 목표









Week1

수업 01-1

강의 자료 및 수업 진행 방식

  1. 강의 자료는 markdown 파일로 작성되어, 홈페이지에내의 lectures 메뉴 게시물을 활용한다. 게시물은 상시로 업데이트가 될 수 있다. 홈페이지 환경에서 ‘theme’을 바꿔 화이트/블랙 모드로 바꿀 수 있다.
  2. 반드시 인터넷 연결 환경을 활용하거나, 미리 수업 자료를 출력해와야 한다. (수업 태도/참여 점수 반영)
  3. 수업 시간에 필요한 개념에 대해 설명하고, 교수자가 필요한 시연을 보인다. 이후 수강생들과 함께 차근차근 실습하거나, 혹은 학생들이 스스로 그리고 혼자서 실습해보길 바란다. :pray:
  4. 강의 자료에 실습 가능한 Python 코드 snippet은 아래와 같은 박스로 표기된다.
print('Hello, world')
  1. 때에 따라서, 기존에 입력한 코드가 이미 실행되어 있어야만 제대로 작동하는 경우가 있으니, 긴장을 늦추지 않고 수업의 진행을 잘 따라오길 바란다.
  2. 수업 시간에 배운 내용을 반드시 스스로 ‘반복’해서 실습해봐야 한다. 그리고 수업 시간내 내어준 예제를 혼자서 해보는 경험이 필요하다.
graph LR
first([개념 설명]) ==> second([교수자 시연]) ==>
third([학생 시연/실습]) ==> fourth([수업후 개념 복습])
==> fifth([수업 후 스스로 혼자 연습])  ==> first

실습 / 코딩

01-1-4 평가 방법

pie title 평가 방법
    "출석" : 40
    "중간고사(Questionary/quiz)" : 20
    "기말고사(maybe final interview/project)" : 20
    "수강/실습/과제 태도 및 참여" : 20

수업 01-2

01-2-1 목표

01-2-2 내용

01-2-3 실습 예시 1

01-2-5 실습 예시 2

01-2-6 실습 예시 3

## 예시
c = float(input("섭씨 온도: "))
f = c * 9/5 + 32
print(f"{c:.2f}C= {f:.2f}F")

01-2-7 실습 예시 4









Week2

수업 02-1

02-1-1. list, tuple, dictionary 생성/수정/조회

02-1-2. List

02-1-3. tuple

02-1-4. set

02-1-5. Dictionary

02-1-6. Misc.

02-1-7 실습.

#세륨의 동위원소는 4가지 존재한다:
# 각 동위원소의 분율은 아래와 같다.
Ce_f= [0.185, 0.251, 88.450, 11.114]  #[%]
# 각 동위원소의 원자량은 아래와 같다.
Ce_w = [135.907, 137.906, 139.905, 141.909]
# 세륨의 평균 원자량은 얼마인가?
avg=(Ce_f[0]*Ce_w[0]+ Ce_f[1]*Ce_w+[1]+ Ce_f[2]*Ce_w+[2]+ Ce_f[3]*Ce_w+[3])/(Ce_f[0]+Ce_f[1]+Ce_f[2]+Ce_f[3])
## average
print(avg)

수업 02-2

02-2-1. if, elif, else 조건문 이해

02-2-2. for 반복문

02-2-3. Built-in function인 range, len, enumerate를 for와 함께 조합!

fruits = ["apple", "banana", "cherry"]

for i in range(len(fruits)):  # 0 ~ len(fruits)-1
   print(f"Index {i}: {fruits[i]}")

specimen_lengths = [10.0, 12.3, 9.8, 11.5]  # cm

for i in range(len(specimen_lengths)):
length = specimen_lengths[i]
   print(f"Specimen {i+1}: {length} cm")

word = "steel"

for i in range(len(word)):
   print(f"Index {i} → {word[i]}")

fruits = ["apple", "banana", "cherry"]

for i, fruit in enumerate(fruits):
   print(i, fruit)

02-2-4. 실습 예시









Week3

수업 03-1 (함수와 클래스 익히기)

03-1-1 함수란


def add(a, b): #함수의 이름이 'add', 입력은 a와 b
   return a + b # 출력은 a+b

def sayhi(): # 함수의 이름이 'sayhi', 입력과 출력 없음
   print('Hi')

def func(a=3,b=5): # 함수의 이름이 'func', 입력 a와 b의 default가 있음.
  """
  a and b are arguments and this function returs a+b
  """
  return a+b

print(func.__doc__) ## docstring 출력
print(help(func))
print(help(help))

def f(a=3,b=5,c,d):
   print(a+b)
   print(c+d)
   return a*b*c*d

03-1-2 built-in functions

03-1-3 class

	class Atom:
		def __init__(self,name):
			self.name = name
		def add_density(self,density):
			self.density=density
		def add_structure(self,structure):
			self.structure=structure

	## usage examples
	myFe=Atom() # Atom 클래스를 활용
	myFe.add_density(7.87) #7.87g/cm^3
	myFe.add_structure('BCC')

	myAl=Atom()
	myAl.add_density(2.70)
	myAl.add_structure('FCC')

03-1-4 클래스 예제

class Alloy:
	def __init__(self, name, tensile_strength, ductility, density):
		self.name = name
		self.tensile_strength = tensile_strength  # MPa
		self.ductility = ductility                # %
		self.density = density                    # g/cm^3

# 합금 데이터
a1 = Alloy("Ni-Cu", 450, 35, 8.9)
a2 = Alloy("Al-Mg", 320, 25, 2.7)
a3 = Alloy("Ti-6Al-4V", 900, 14, 4.4)

alloys = [a1, a2, a3]

# 특정 물성(property) 가져오기
property_to_check = "tensile_strength"  # 여기만 바꾸면 됨

for alloy in alloys:
	  value = getattr(alloy, property_to_check, "N/A")
	  print(f"{alloy.name}: {property_to_check} = {value}")

03-1-5 여러 함수 만들어 보기

수식을 Python함수로 만들려면, 각 물리량을 뜻하는 기호에 적당한 이름을 붙여 변수로 지정해야 겠다. 나는 앞의 예제에서, 우선 첫번째로, 함수의 이름을 hooke이라 지었다. 그리고 변형률을 저장할 변수를 그에 해당하는 기호 $\varepsilon$ (epsilon)을 말 그대로 epsilon이라 지었고, 탄성계수(elastic modulus)에서 modulus를 사용했다. 같은 함수를 아래와 같이 작성할 수 있고, 정확히 같은 기능을 수행한다. 하지만, 전혀 추천되지 않는 이름들을 사용했다. 프로그램이 작고 간단할 때는 큰 문제가 되지 않을 수 있으나, 점점 프로그램이 커지고 복잡해지면 이와 같은 너무 간단한 이름은 선언될 때 본디 뜻하던 변수를 기억하기 쉽지 않고, 실수를 범하게 쉽게 만든다.

def a(b,c):
return a*b

수업 03-2 (모듈 만들기)

03-2-1 개념

03-2-2 실습

03-2-3. ex 01: 간단한 모듈 만들기 (더하기 곱하기)

  1. 모듈 작성
# 아래 모듈을 작성 후 mymodule.py로 저장하자.
def add(valuea, valueb):
	  return valuea + valueb

def multiply(valuea, valueb):
	  return valuea * valueb

def power(valuea, valueb):
	  return valuea ** valueb
  1. 그 다음 아래를 활용해 mymodule을 불러와 보자.
import mymodel
mymodule.add(3,4)
mymodule.multiply(3,4)
mymodule.power(3,4)
  1. etc

03-2-4. ex 02: CLI에서 arguments 받기

예제









Week4





수업 04-1 기초 (file/IO)

04-1-1. 개념

Python에서 파일을 통한 I/O는 open() 함수 활용한다 (자세한 설명은 여기를 참고바람). open함수를 통해 파일 오브젝트를 생성하고, 이를 통해 파일로 data를 입력하거나, 파일로부터 data를 불러올 수 있다. open의 경우 파일을 여는 여러가지 모드가 있다. open함수에 arguments로 filename을 입력하고, 모드를 지정한다.

04-1-2. 예시

문자열 포매팅

퍼센트 (%) 방식

문자열에 %s, %d, %i, %f기호를 삽입하여 문자나 값을 대체하여 넣을 수 있다. 아래 예문을 보면, name과 density를 print가 되는 문자열 속에 특정 위치에 삽입 후 출력하는 것을 확인할 수 있다.

name='Iron'
density=7.87
print('The density of %s is %d g/cm^3'%(name,density))

문자열 속의 실수(float)의 경우 소수점자리를 수정하여 표현할 수 있다. 아래 예제를 살펴보면, 첫번째 print문은 소수점 첫째자리까지, 그리고 두번째 print는 소수점 다섯째자리까지 출력하는 것을 확인할 수 있다.

print('9 / 6 = %.1f'%(9/6))
print('9 / 6 = %.5f'%(9/6))

str.format()는 다루지 않겠다.

f-string

%를 활용한 방법만큼 널리 쓰이는 포매팅 기법은 f-string 기법이다. 아래와 같이, 문자열이 시작되는 따옴표에 앞서 f로 f-string형식을 활용함을 밝히고, 문자열내에 { 및 }쌍 내부에 변수의 이름을 직접 적는 방식이다. %기법은 대체되는 변수가 문자열 바깥에 기입되는 반면, f-string은 문자열 내부에 기입되어 있어 코드를 읽기가 더욱 수월하다는 장점이 있다.

print(f'9/6 = {9/6:.1f}')
print(f'9/6 = {9/6:.5f}')
val=9/6
print(f'9/6 = {val:.1f}')
print(f'9/6 = {val:.5f}')

파일 쓰기 연습

1에서부터 100까지 모든 정수가 한줄에 하나씩 쓰여진 파일을 만들어보자. 반복되는 작업이 예상되므로 for구문이 필요하겠다. 아래와 같은 코드를 화면에 출력하게 되겠다.

for i in range(1,101):
   print(i)

화면에 출력하지 않고, 파일 one2hund.txt를 만들어 같은 방식의 출력을 다음과 같은 예시를 통해 수행할 수 있다.

myfile = open('one2hund.txt','w') # file 열기
for i in range(1,101):
  myfile.write(f'{i}') # myfile instance의 write method 활용
myfile.close() # file 닫기

이후 파일을 열어보면, 가로로 모든 숫자가 붙은채로 아래와 유사하게 출력되는 것을 확인할 수 있다.

123456789101112131415161718...

각각의 정수를 개개의 줄로 출력이 되게끔 줄바꿈기호 ‘\n’를 활용하여 파일에 출력해보자.

myfile = open('one2hund.txt','w') # file 열기
for i in range(1,101):
  myfile.write(f'{i}\n') # myfile instance의 write method 활용
myfile.close() # file 닫기

파일을 열기(open)하고 닫지 않는다면 예상하지 못한 일이 발생할 수 있다. 따라서 파일 오브젝트를 open으로 생성한 뒤, 쓰임이 다하면 close메소드로 닫아야 한다. 따라서, open과 close는 짝으로 쓰일때가 많다. open 활용 이후 close구문을 깜빡하지 않게 강제시켜주는 좋은 습관은 with구문을 함께 활용하는 것이다. 아래 에제를 보자.

with open('one2hund.txt','w') as myFile # file 열기
   for i in range(1,101):
      myfile.write(f'{i}\n') # write method 활용

with와 indented된 구역으로 나누어 구성되어, 더욱 세련되게 코드 작성을 도와주고 읽기 쉽게 만들어준다.

파일 읽기 연습

위 쓰기에 이어서, 생성된 파일을 읽어보자.

myfile= open('one2hund.txt','w') # file 열기
for i in range(1,101):
  myfile.write(f'{i}\n') # myfile instance의 write method 활용
myfile.close() # file 닫기

myfile = open('one2hund.txt','r') # file 열기
cnt=myfile.read()
print(cnt)





수업 04-2 (NumPy 기초)

기초 개념

불행하게도, 많은 인터넷 자료가 그렇듯이, 문서가 영어로 작성되어 있다. 다행히도 최신 브라우저들은 번역 기능이 탑재되어 있으니 활용하면 좋겠다.

앞서 List를 활용하여, math package를 함께 사용하면, 스칼라, 벡터, 행렬 등을 대상으로 다양한 수학적 연산을 수행할 수 있다. 하지만 Python의 built-in 기능으로는 빠른 수학적 연산처리가 어렵다. 이를 보완하고자 연산속도가 빠르면서도 다양한 수학적 기능을 도와주는 NumPy패키지가 개발되었다. NumPy설치를 위해서는 pip를 활용할 수 있다. 인터넷이 연결된 컴퓨터의 CLI환경에서 다음과 같이 명령어를 입력하면 설치가 가능하다. 인터넷으로 연결된 시스템의 터미널에서 아래와 같이 입력하면 설치된다.

c:/users/user/myrepo> pip install numpy

이후 파이썬 환경에서 NumPy패키지를 import해 사용하면 되겠다. 많은 경우, 아래와 같이 np라는 이름으로 불러오는 경우가 많다.

import numpy as np

다른 많은 Python 패키지들과 마찬가지로, open source 프로젝트로 개발되었으며, 현재로 활발히 업데이트가 되고 있다. 따라서 새로운 기능이 추가되거나, 종전의 기능이 없어지는 경우가 있으므로, 어떠한 버전을 활용하고 있는지 확인이 필요할 때가 있다. 그리고 한 시스템내에서 다양한 위치에 서로다른 패키지가 설치될 때가 있으므로, 사용되는 NumPy패키지의 위치를 확인할 필요가 있다. 아래의 두 경우를 살펴보자.

import numpy as np
print(np.__version__)
print(np.__file__)

List로 생성된 값의 모임을 간단히 NumPy배열 형식 numpy.ndarray로 간편히 바꿀 수 있다. 아래 예시들을 살펴보자.

# 1차원 배열
arr1 = np.array([1, 2, 3])  # np.array 클래스 생성.
print(arr1)

# 2차원 배열
arr2 = np.array([[1, 2, 3], [4, 5, 6]])
print(arr2)

# 0으로 채운 배열
zeros_arr = np.zeros((2, 3))  # zeros method활용하여 2x3배열
print(zeros_arr)

# 1로 채운 배열
ones_arr = np.ones((3, 3)) # 3x3배열
print(ones_arr)

# 특정 값으로 채운 배열
full_arr = np.full((2, 2), 7)
print(full_arr)

# 연속된 수
range_arr = np.arange(0, 10, 2)  # 0부터 10 전까지 2씩 증가
print(range_arr)

# 랜덤 배열
rand_arr = np.random.rand(2, 3)  # 0~1 사이 난수
print(rand_arr)

numpy.ndarray형식은 NumPy의 array클래스의 instance로써, 다양한 속성(attributes)와 매서드(method) 갖고 있다. 아래의 attributes와 매서드가 자주 쓰인다. 그 쓰임을 익힐 필요가 있다.

arr = np.array([[1, 2, 3], [4, 5, 6]])
print(arr.shape)   # (2, 3) → 2행 3열
print(arr.ndim)    # 차원 수 → 2
print(arr.size)    # 전체 원소 개수 → 6
print(arr.dtype)   # 데이터 타입 → int64 (환경에 따라 다름)
print(arr.ravel()) ## memory-efficient
print(arr.flatten()) ## independent copy
print(arr.ravel().sum())
print(arr.flatten().sum())

NumPy의 배열간의 연산은 벡터화되어 속도가 빠르다. 많은 경우, for, range 등의 일반적인 반복문 필요없어, 간단한 형태로 표기되어, list를 활용한 것보다 수식 표현과 연산속도에 유리하다.

a = np.array([1, 2, 3])
b = np.array([4, 5, 6])

print(a + b)   # [5 7 9]
print(a - b)   # [-3 -3 -3]
print(a * b)   # [ 4 10 18]  (요소별 곱)
print(a / b)   # [0.25 0.4 0.5]
print(a ** 2)  # [1 4 9]    (제곱)


## 각각의 경우 List를 활용했을 때 훨씬 많은 코딩 필요함.
c=[] # +
for i in range(a):
  c.append(a[i]+b[i])

c=[] # -
for i in range(a):
  c.append(a[i]-b[i])

c=[] # *
for i in range(a):
  c.append(a[i]*b[i])

c=[] # /
for i in range(a):
  c.append(a[i]/b[i])

c=[] # **
for i in range(a):
  c.append(a[i]**2)

##?
print((a**2).sum())

List를 활용한 방식과 NumPy의 속도 비교를 위해 아래 예제를 활용해보자. 우선 0에서부터 100까지 정수가 담겨있는 List와 numpy.ndarray 형식의 자료를 만들자.

mylist=list(range(101))
mylist ## The list type object
myarray=np.array(mylist)
myarray ## The numpy type object

아래와 같이 각각의 연산을 JuPyter의 매직 키워드 %%timeit를 활용해 7번 반복 연산해 평균 연산 속도를 측정해보자.

%%timeit
s=0.
for i in range(100):
    s=s+mylist[i]

그리고 sum 매소드를 활용한 결과를 비교해보자.

%%timeit
s=myarray.sum()

나의 경우에는 전자는 \(1.85 \mu s = 1.85 \times 10^{-6} s\) 그리고 후자는 \(539 ns = 538\times 10^{-9} s = 0.538 10^{-6} s\) 결과가 나왔다. 후자는 전자에 비해 약 1/3 정도의 시간만 필요하였다.

차원과 축: NumPy 배열을 바라보는 두가지 관점

NumPy배열의 ‘차원’(dimension, 혹은 rank)는 배열이 몇 겹으로 중첩되어 있는지를 의미한다. 쉽게 말해, 데이터가 몇 단계의 리스트로 레이어로 감싸져 있는지에 따라 차원이 달라진다. 아래를 살펴보자.

import numpy as np

a = np.array(5)                  # 스칼라 (0차원)
b = np.array([1, 2, 3])          # 벡터 (1차원)
c = np.array([[1, 2, 3],
              [4, 5, 6]])        # 행렬 (2차원)
d = np.array([[[1], [2], [3]],
              [[4], [5], [6]]])  # 행렬 (3차원) ... 혹은 ML/AI 관련 문헌에서 '텐서'라 불림 - 수학/물리 문헌의 '텐서'와 다름.
print(a.ndim)
print(b.ndim)
print(c.ndim)
print(d.ndim)

차원과 다르게 ‘축’(axis)의 관점에서 배열을 바라보는 관점도 있다. 이때 ‘축’은 배열의 index방향을 의미한다. 즉, 다차원 배열에서 데이터를 접근하거나 연산할 때 어느 방향을 기준으로 하느냐에 따라 축이 달라진다. 다음 배열은 차원의 관점에서는 2차원임을 알 수 있다.

c = np.array([[1, 2, 3],
              [4, 5, 6],
              [7, 8, 9]])

이 경우 축이 2개인 것으로 이해할 수 있다. 첫번째 축 0은 행을 따라 내려가는 방향 (세로, column-wise)이 되며, 축 1은 열을 따라 가로로 가는 방향 (가로, row-wise)로 이해된다. 아래 각 열, 그리고 행 ‘축’을 따라 덧셈을 하는 경우를 살펴보자.

c = np.array([[1, 2, 3],
              [4, 5, 6],
              [7, 8, 9]])
print(c.sum(axis=0))  # 열별 합 → [12 15 18]
print(c.sum(axis=1))  # 행별 합 → [ 6 15 24]

3D 배열에서 축 번호는 ‘바깥’부터 ‘안쪽’ 순으로 0, 1, 2, … 순으로 이어진다.

d = np.array([[[1, 2], [3, 4]],
              [[5, 6], [7, 8]]])

d.shape은 (2,2,2)이고, d.ndim은 3이다. 즉 3차원이고, 총 세 축으로 이루어진다. 각 축을 따라 2개씩 element가 있는 구조로 이해할 수 있다. 이때

아래 경우를 더 살펴보자.

a = np.arange(15)

위 결과로 1D 배열에 0에서부터 14까지 15개의 element 숫자가 자료가 a에 저장된다. 이를 (3x5) 형태의 2D 배열로 형태를 바꿀 수 있다. reshape method를 활용한다.

b=a.reshape(3,5)

이때 두 축이 활용된 것으로 볼 수 있고, 첫번째 축 axis=0은 3 요소를, 두번째 축 axis=1은 5 요소를 가진 것으로 이해할 수 있다. 그 결과를 b로 저장했고 그 결과를 출력해보자

print(b)

다음과 같이 출력이 될것이다.

array([[ 0,  1,  2,  3,  4],
       [ 5,  6,  7,  8,  9],
       [10, 11, 12, 13, 14]])

첫번째 축(axis=0)의 첫 요소는 [0,1,2,3,4], 그 다음은 [5,6,7,8,9], 마지막 세번째는 [10,11,12,13,14]가 된다. 이를 인덱싱 해보면

print(b[0,:])
print(b[1,:])
print(b[2,:])

이번에는 두번째 축 (axis==1)을 따라 살펴보자. 첫 요소는 [0,5,10], 그 다음은 [1,6,11], [2,7,12], [3,8,13], 마지막 5번째 요소는 [4,9,14]가 될 것이다.

print(b[:,0])
print(b[:,1])
print(b[:,2])

Indexing & slicing

List 타입의 자료에서도 indexing과 slicing이 사용된다. [시작,끝,스텝]형태의 인덱싱이 NumPy 배열에도 동일하게 적용된다.

mylist=List((3,3,4,3,3,4,5,6))
#mylist[시작:끝:스텝] 형태로 index가 적용되는 것 처럼 ..

myarray=np.array((3,3,4,3,3,4,5,6))
myarray[2:6:2] #3번째부터 6번째까지, 2칸씩 띄어 넘으며 ..
#mylist[시작:끝:스텝] 형태로 index가 적용되는 것 처럼 ..

위 결과는 아래와 같을 것이다.

array([ 5, 10])

NumPy 배열에 경우에는 이러한 indexing이 각 ‘축’에 깔끔히 적용될 수 있다. 아래 2차원 배열 (혹은 2축으로 구성된 배열)을 살펴보자.

arr = np.array([[1, 2, 3], [4, 5, 6]])

위의 경우, 첫번째 축(axis=0)은 2개의 요소 그 다음 축(axis=1)은 3개의 요소로 이루어진 것을 알 수 있다. 즉

# nested 배열의 각 축을 '행'(가로)과 '열'(세로)이라 하면
# arr = [  1  2  3 ] # 첫번째 가로
#.         4  5  6   # 두번째 가로

print(arr[0, 0])  # 1행 1열 → 1
print(arr[1, :])  # 2행 전체 → [4 5 6]
print(arr[:, 1])  # 모든 행의 2열 → [2 5]

각 축마다 begin, end, step이 적용되므로, 복잡한 slicing을 할 수 있다. 아래를 보자.

## 각 '축'에서 List indexing 적용가능. 예를 들어
print(arr[1::,1::])
print(arr[::2,::2])

#
print(arr[::-1,::])  #행만 거꾸로
print(arr[::,::-1])  #열만 거꾸로
print(arr[::-1,::-1]) #행과 열을 모두 거꾸로

아래 경우를 하나씩 입력 후 차근차근 살펴보며 실습해보자.

a=np.arange(100)
a=a.reshape(10,10)
a[:,::2]  # 각 10자리에서 짝수로만 이루어진 2차원 배열
a[0::2,::] # 10자리수가 짝수로 이루어진 2차원 배열
a[1::2,::] # 10자리수가 홀수로 이루어진 2차원 배열
a[::,1::2] # 1의 자리수가 홀수로 이루어진 2차원 배열
a[::,0::3] # 1의 자리수가 0, 3, 6, 9로 끝나는 수로 이루어진 2차원 배열
a[0::3,::] # 10의 자리수가 0, 3, 6, 9로 끝나는 수로 이루어진 2차원 배열

다음 3차원의 경우도 살펴보자.

a=np.arange(1000)
a=a.reshape(10,10,10) #
a[::5,::,::] #?

# 행렬 저장하기 (공백 구분)
matrix = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])
np.savetxt("save_matrix.txt", matrix, fmt="%.2f")

# CSV로 저장
np.savetxt("save_matrix.csv", matrix, delimiter=",", fmt="%d")









Week5

수업 05-1 (List활용한 기초 행렬 연산)

05-1-1. 기본 예제 (벡터의 크기, 내적, )

3차원 벡터는, 가령 아래와 같이 세 성분으로 이루어져 있으며,

\[\boldsymbol a=(a_1,a_2,a_3)\]

그 크기는 다음과 같이 정의된다.

\[|\boldsymbol a|=\sqrt{a_1^2+a_2^2+a_3^2}=\sqrt{\sum_i^3a_i^2}.\]

주어진 벡터 v의 크기를 구하는 함수 get_mag를 아래의 예와같이 작성될 수 있겠다.

def get_mag(v):
   import math
   return math.sqrt(v[0]**2+v[1]**2+v[2]**2)

주어진 벡터를 3차원에서 벗어나 n차원 공간으로 일반화 한다면 (Frobenius norm)정의를 활용해 다음과 같이 표현할 수 있다.

\[|\boldsymbol a|=\sqrt{\sum_i^na_i^2}\]

이를 다시 다음과 같은 파이썬 코드 예시로 작성할 수 있겠다.

def frob(vector):
   import math
   s=0. # sum
   for i, e in enumerate(vector):
      s=s+e**2
   return math.sqrt(s)

두 벡터 $\boldsymbol a$와 $\boldsymbol b$의 내적은 다음과 같이 정의된다.

\[\boldsymbol a \cdot \boldsymbol b=a_1b_1+a_2b_2+a_3b_3=\sum_i^3a_ib_i\]

혹은 아래와 같이 두 벡터 사이의 끼인 각 $\theta$를 활용해 표현할 수 있다.

\[\boldsymbol a \cdot \boldsymbol b=|\boldsymbol a||\boldsymbol b|\cos\theta\]

두 벡터 사이의 내적을 list, len, range, enumerate 등을 활용하여 아래와 같이 표현 가능하다.

a=[1,2,3]
b=[4,5,6]
dotprod=0.
for i in range(3):
   dotprod=dotprod+a[i]*b[i]
   ## 위를 `dotprod+=a[i]*b[i]`로 줄여서 표현 가능

NumPy의 배열을 활용한다면 위를 더욱 축약 시킬 수 있다.

a=np.array([1,2,3])
b=np.array([4,5,6])
dotprod=0.
for i in range(len(a)):
   dotprod+=a[i]*b[i]
print(dotprod)

혹은 위를 더 축약 시켜

a=np.array([1,2,3])
b=np.array([4,5,6])
dotprod=0.
print((a[i]*b[i]).sum())

혹은 @을 활용하여 다음과 같이 더욱 축약하여 작성할 수 있다.

a=np.array([1,2,3])
b=np.array([4,5,6])
print(a@b)

두 3D 벡터가 주어졌을 때 사이 끼인 각을 구하려면, 앞서 활용된 서로다른 두 벡터의 정의를 함께 활용할 수 있다. 즉

\[\boldsymbol a \cdot \boldsymbol b=a_1b_1+a_2b_2+a_3b_3=\sum_i^3a_ib_i=|\boldsymbol a||\boldsymbol b|\cos\theta\]

위 식을 정리하여 활용하면 아래와 같다.

\[\frac{a_1b_1+a_2b_2+a_3b_3}{|\boldsymbol a||\boldsymbol b|}=\cos\theta\]

따라서

\[\theta=\cos^{-1}\bigg(\frac{a_1b_1+a_2b_2+a_3b_3}{|\boldsymbol a||\boldsymbol b|}\bigg)\]

위를 math모듈과 그 모듈내의 sqrt, acos을 활용하여 아래와 같은 간단한 코드를 작성할 수 있다.

def get_mag(v):
   import math
   return math.sqrt(v[0]**2+v[1]**2+v[2]**2)

def get_ang(a,b):
   import math
   dotprod=0.
   for i in range(len(a)):
      dotprod+=a[i]*b[i]
   costh=dotprod/(get_mag(a)*get_mag(b))
   print(f'costh:{costh}')
   th=math.acos(costh)
   return th

a=[1,0,0]
b=[0,1,0]
angle=get_ang(a,b)
print('ang in radian:', angle)
## angle to degree?
print('ang in degree:', angle*180/3.141592)

05-1-2. 2x2 행렬간의 dot product 이해하기

두 행렬의 곱을 이해해보자. 행과 열이 각각 (l,m)인 행렬

\[\boldsymbol{A}_{l\times m}\]

와 (m,n)인

\[\boldsymbol{B}_{m\times n}\]

의 곱은 새로운 행렬이 된다. 새로운 행렬을 \(\boldsymbol{C}\)라 하면, 그 행렬의 행과 열은 (l,n)이 되며 다음과 같이 표기되곤 한다.

\[\boldsymbol{C}=\boldsymbol{A}\cdot\boldsymbol{B}\]

이때, 앞선 행렬의 한 행의 요소와, 뒷따르는 행렬의 열 요소들이 각기 순서대로 곱해져서 새로운 행렬 $\boldsymbol{C}$를 이루게 되며, 그 방식이 아래 그림에 표기되어 있다.

<img src=https://upload.wikimedia.org/wikipedia/commons/e/eb/Matrix_multiplication_diagram_2.svg />

예를 아래 두 벡터의 곱의 예를 함께 살펴보자,

\[\begin{bmatrix} 1 & 2 \\ 3 & 4 \end{bmatrix} \cdot \begin{bmatrix} 2 & 0 \\ 1 & 3 \end{bmatrix} = ?\]

두 2x2 행렬 \(\boldsymbol A\)와 \(\boldsymbol B\)를 곱하여 행렬 \(\boldsymbol C\)가 된다면, 아래와 같이 표현한다.

\[\boldsymbol C = \boldsymbol A \cdot \boldsymbol B\]

이 때

\[\begin{array}{c} C_{11}=A_{11}B_{11}+A_{12}B_{21} \\ C_{12}=A_{11}B_{12}+A_{12}B_{22} \\ C_{21}=A_{21}B_{11}+A_{22}B_{21} \\ C_{22}=A_{21}B_{12}+A_{22}B_{22} \\ \end{array}\]

가 된다. 이를 그대로 Python으로 옮기면

A = [[1, 2], [3, 4]]
B = [[2, 0], [1, 3]]

C=[[0,0],[0,0]]
C[0][0]=A[0][0]*B[0][0]+A[0][1]*B[1][0]
C[0][1]=A[0][0]*B[0][1]+A[0][1]*B[1][1]
C[1][0]=A[1][0]*B[0][0]+A[1][1]*B[1][0]
C[1][1]=A[1][0]*B[0][1]+A[1][1]*B[1][1]
print('1:',C)

위 행렬곱 식에서 \(\boldsymbol{C}\)행렬 요소 위치에 따라 달라지는 \(\boldsymbol{A}\)와 \(\boldsymbol{B}\)행렬의 위치가 있다. 이를 살펴보면

\[C_{ij}=A_{i1}B_{1j}+A_{i2}B_{2j}\]

로 표현됨을 알 수 있다. 이를 반영하여 모든 \((i,j)\) 짝에 적용하면…

A = [[1, 2], [3, 4]]
B = [[2, 0], [1, 3]]

C=[[0,0],[0,0]]
i=0;j=0
C[i][j]=A[i][0]*B[0][j]+A[i][1]*B[1][j]
i=0;j=1
C[i][j]=A[i][0]*B[0][j]+A[i][1]*B[1][j]
i=1;j=0
C[i][j]=A[i][0]*B[0][j]+A[i][1]*B[1][j]
i=1;j=1
C[i][1]=A[i][0]*B[0][j]+A[i][1]*B[j][1]
print('2:',C)

그런데, 코드를 살펴보면, 아래의 동일한 statements가 4번 반복되는 것을 알 수 있다.

C[i][j]=A[i,0]*B[0,j]+A[i,1]*B[j,1]

\((i,j)\)가 각각 for구문을 통해 0,1을 반복하므로, 아래와 같이 축약할 수 있겠다.

A = [[1, 2], [3, 4]]
B = [[2, 0], [1, 3]]

C=[[0,0],[0,0]]
for i in range(2):
    for j in range(2):
        C[i][j]=A[i][0]*B[0][j]+A[i][1]*B[1][j] ## 네 statements가 동일함에 주목!
print('3:',C)

그런데, 반복되던 statement의 우변에서도 0과 1이 반복된다.

C[i][j]=A[i][0]*B[0][j]+A[i][1]*B[j][1]

따라서

for k in range(2):
   C[i][j]=C[i][j]+A[i][k]*B[k][j]

라 줄일 수 있겠다. 이렇게 모두 줄일 수 있는 만큼 줄여서 축약된 형태로 표현하면 ..

#더 줄이면?
C=[[0,0],[0,0]]
for i in range(2):
	for j in range(2):
		for k in range(2):
			C[i][j]=C[i][j]+A[i][k]*B[k][j]
			#C[i][j]+=A[i,k]*B[k,j]      += 기호 사용
print('4:',C)

두 2x2행렬 곱은, 아래 더 상세히 배우게 될 NumPy패키지를 활용하면 더욱 축약된 형태로 작성가능하다.

import numpy as np
A = np.array([[1, 2], [3, 4]])
B = np.array([[2, 0], [1, 3]])
print('6:',A @ B)          # 행렬 곱
print('7:',np.dot(A, B))   # 동일

05-1-3. 두 3x3 행렬 곱? 일반화하여, nxn 행렬사이의 곱은?

\(\boldsymbol A\) 와 \(\boldsymbol B\) 의 곱 결과가 또 다른 3x3행렬 \(\boldsymbol C\) 이라면

\[\boldsymbol A\cdot\boldsymbol B = \boldsymbol C\]

와 같이 표현할 수 있다. 이를 index를 활용한 방식으로 아래와 같이 표기 가능하다.

\[\sum_k^3A_{ik}B_{kj}=C_{ij}, \text{ for } i=1,2,3 \text{ and } \ j=1,2,3\] 
# for loop 3개를 활용해서 표현할 수 있겠는가?

# 두 nxn 행렬 사이의 곱을 구하는 python 함수를 작성해 보세요.
\[\boldsymbol D=\boldsymbol A \cdot \boldsymbol B \cdot \boldsymbol C\]

이를 인덱스 notation으로 표현하면

\[D_{ij}=A_{ik}B_{kl}C_{lj}=\sum_k\sum_l A_{ik}B_{kl}C_{lj} \text{ for } (i,j) = (1,1), (1,2), ..., (3,3)\] 
# 세 nxn 행렬 사이의 곱을 구하는 python 함수를 작성해 보세요.

05-1-3. 외적

05-1-4. Broadcasting

05-1-5. Other various features

arr = np.array([1, 4, 9, 16])

print(np.sqrt(arr))   # 제곱근 → [1. 2. 3. 4.]
print(np.exp(arr))    # e^x
print(np.log(arr))    # 자연로그
print(np.sin(arr))    # 사인 함수
print(np.mean(arr))   # 평균
print(np.sum(arr))    # 합
print(np.min(arr))    # 최소값
print(np.max(arr))    # 최대값
print(np.std(arr))    # 표준편차

arr = np.array([3, 1, 2])

print(np.sort(arr))        # 정렬된 배열
print(np.argsort(arr))     # 정렬 인덱스
print(np.argmax(arr))      # 최대값 인덱스
print(np.argmin(arr))      # 최소값 인덱스

ind=np.argsort(arr)
arr[ind] ## sorting 이 된 배열

# 추가 예제
names=['Michael','Jim','Pam','Dwight','Kevin','Creed']
scores=[5, 30, 20, 40, 10, 25]

inds=np.argsort(scores)
print(names[inds]) ## score에 따라 정렬된 배열

수업 05-2 아인슈타인 표기법과 np.einsum 함수

Reference: https://rockt.ai/2018/04/30/einsum

아인슈타인 표기법은, 벡터, 행렬, 텐서가 사용된 수학 수식에서, 중복된 기호와 합기호 $\sum$가 함께 나타나는 연산을 표기할 때, 합기호를 생략하는데 착안하여 복잡한 수식을 좀 더 간략하게 표기하는 방식이다. 아래 수식에서 한 기호가 하나의 값을 표현할 때는 굵지 않은 글씨체로 ($a$), 만약 벡터와 같이 하나의 기호가 여러 값으로 이루어져 있을 때는 굵은 글씨체 ($\boldsymbol a$)로 표기하겠다.

05-2-1 다양한 행렬 그리고 벡터 연산과 Einstein 표기법

벡터 스케일링 (스칼라 곱)

주어진 벡터 $\boldsymbol a$에 스칼라 $c$를 곱하면 또 다른 벡터 $\boldsymbol b$이 된다. 이는 아래와 같이 수식으로 표현가능하다.

\[c\boldsymbol a=\boldsymbol b\]

이를 index 표기법으로 나타내면, 3차원 공간에서 각 벡터는 3성분을 지니므로, 아래 첨자 $_i$를 활용해 각 첨자를 구분할 수 있다. 즉 벡터 $\boldsymbol a$는 사실 $(a_1,a_2,a_3)$로 구분되는 세 성분으로 이루어져 있으며, 이는 벡터 $\boldsymbol b$도 마찬가지이다. 따라서 앞선 수식을 각 성분에 대해 나타낸다면, 각기 구분되는 세 수식 $b_1=ca_1$ 그리고 $b_2=ca_2$, 마지막으로 $b_3=ca_3$으로 대신할 수 있다. 그런데, 아무래도 이건 조금 번거로운 느낌이 든다. 아래와 같이 좀 더 간략하게 표기하는 게 좋겠다.

\[b_i=ca_i \text{ with } i=1,2,3\]

위를 Python의 List, 그리고 NumPy를 가지고 각기 표현할 수도 있겠다.

벡터의 크기

벡터의 크기는 앞서 이미 다루었다. 한 벡터 $\boldsymbol a$의 크기는 $ \boldsymbol a $라 표기하고, 이는 다음과 같이 정의된다.
\[|\boldsymbol a|=\sqrt{\sum_i^3a_i^2}\]

고전적인 아인슈타인 표기법은 위와 같이 하나의 물리량에 일반적으로 적용되진 않는다. 하지만 NumPy의 einsum 함수는 적용된다. 아래와 같이 먼저 벡터내의 요소의 거듭제곱으로 이루어진 벡터를 구할 수 있다. 벡터 $\boldsymbol a$가 가령 아래와 같다고 하자. \(\boldsymbol a= (2,3,4)\)

import numpy as np
a=np.array([2,3,4])

만약 2+3+4를 구하는게 목적이라면, 즉 $\sum_i a_i$가 목적이라면, 아래와 같이 수행할 수 있다.

np.einsum('i->',a)

그런데 우리는 $\sum_ia_i^2$을 먼저 구해야 하겠다. 따라서 아래와 같이 약간 변화를 줄 수 있다.

np.einsum('i->',a**2)

다음으로 이렇게 얻어진 값의 제곱근을 구해야 하므로 아래가 최종적으로 적절한 형식이 되겠다.

np.sqrt(np.einsum('i->',a**2))

단위 벡터 (unit)

벡터 $\boldsymbol a$의 크기가 1 이라면 (즉 $|\boldsymbol a=1|$), 벡터 $\boldsymbol a$ 를 단위 벡터(unit vector)라 부른다. 즉 단위 벡터란, 크기가 1인 벡터를 뜻한다. 주어진 한 벡터 $\boldsymbol a$의 단위 벡터를 $\bar{\boldsymbol a}$라 할 때, $\boldsymbol a$와 $\bar{\boldsymbol a}$의 관계를 다음과 같이 표현할 수 있다:

\[\bar{\boldsymbol a}=\frac{\boldsymbol a}{|\boldsymbol a|}\]

앞서 스칼라곱에서 보았듯, 마찬가지로 개별 성분값들을 활용한 index표기법을 활용해 아래와 같이 표현할 수 있다.

\[\bar{a}_i=\frac{a_i}{\sqrt{a_1^2+a_2^2+a_3^2}}\]

위 수식도 사실은 $i$가 1, 혹은 2, 혹은 3인 세 경우에 각기 해당하는 수식을 의미한다. 즉 위는 아래 표기법과 같이

\[\bar{a}_i=\frac{a_i}{\sqrt{a_1^2+a_2^2+a_3^2}}, \text{ with } i=1,2,3\]

의 $i=1,2,3$ 부분이 생략된 것이라 볼 수 있다. 정리하자면 아래 탭에 세가지 각기 다른 방식으로 표현된 수식들은 사실 모두 동일한 수식을 표현하고 있는 것이다.

index를 활용하되 아무런 생략없이 표기된 경우(생략없이)와 비교했을 때, WITH생략의 경우 얼마나 많이 수식에 활용된 표현이 축약될 수 있는지 비교해보자. 그리고 생략 되어 표기된 경우만 주어지더라도, 생략되지 않은 경우를 의미하는 바를 잘 파악할 수 있어야 하겠다. 굵은 글씨체로 표기된 경우가 가장 많이 생략된 표기법이나, index가 사용되지 않아 수식의 명확성이 높지 않을 수 있다. 마지막에 완전히 생략된 표기법은 Einstein 표기법을 이해하기 위한 기초가 된다.

예시:

주어진 벡터 \(\boldsymbol a\)와 방향은 같으나 크기가 1인 단위 벡터를 구하는 Python 예제를 살펴보자.

예시: 반대방향 벡터

한 벡터 $\boldsymbol a$와 크기가 같으나, 방향이 반대인 벡터를 $\boldsymbol b$라 한다면, 아래와 같은 결과를 얻는다.

예시: 벡터의 합

예시: 벡터의 차

내적 (inner dot)

두 벡터간의 ‘내적’이라 일컫는 연산의 결과는 스칼라가 된다.

\[\boldsymbol a \cdot \boldsymbol b = \sum_i^3 a_ib_i=c\]

위를 Einstein summation convention으로 표기하면

\[\boldsymbol a \cdot \boldsymbol b = a_ib_i=c\]

Einstein 표기법에 따르면, 앞서 $\text{ with } i=1,2,3 $가 생략되었듯, summation 기호 \(\sum_i^3\)가 생략되어 표기된다. 정리하자면, 두 벡터간의 내적에서 ‘곱’이 나타난 경우, 곱셈의 대상이 되는 두 물리량의 인덱스가 동일하게 표기된다 (위 에서는 $i$). 중복된 인덱스 $i$가 나타나면 summation기호가 같이 표현되므로, 중복된 인덱스가 나타날 때, 필연적으로 summation이 수행됨을 예상할 수 있다. 이러한 생각이 summation기호를 생략하는데 이르게 된다.

(nxn)행렬과 (n)벡터 곱

행과 열이 각각 n인 행렬과 (즉 nxn행렬)과 n성분으로 구성된 벡터간의 곱

\[\boldsymbol c = \boldsymbol A \cdot \boldsymbol v\]

이 index를 활용해 다음과 같이 표기된다.

\[c_i = \sum_j^nA_{ij}v_j \ \text{ for } i=1,2,...,n\]

위 결과를 정리하자면 아래와 같다.

행렬 곱1 (single dot)

두 행렬 $\boldsymbol A$와 $\boldsymbol B$의 곱이 아래와 같이 정의된다고 하자.

\[C_{ij} = \sum_k^3 A_{ik}B_{kj} \text{ for } (i,j) \text{ of } (1,1), (1,2), ... , (n,n-1), (n,n)\]

아래 결과로 정리된다.

행렬 곱2 (double dot)

\[c=\boldsymbol A : \boldsymbol B\] \[\rightarrow c=\sum_i\sum_jA_{ij}B_{ij}=\sum_j\sum_iA_{ij}B_{ij}=\sum_j\sum_iB_{ij}A_{ij}=\sum_i\sum_jB_{ij}A_{ij}\]

파이썬 코드로 바꾸면…

A=[[1,2,3],[4,5,6],[7,8,9]]
B=[[3,2,1],[6,5,4],[9,8,7]]
## 1
c=0.
for i in range(3): # i is outer
  for j in range(3): # j is inner
	  c+=A[i][j]*B[i][j]
print(c)
## 2, 안/바깥 for-loop 바뀜.
c=0.
for j in range(3): # j is outer
  for i in range(3): # i is inner
    c+=A[i][j]*B[i][j]
print(c)
## 3. 안/바깥 for-loop 바뀜, 그리고 A와 B의 순서 바뀜
c=0.
for j in range(3): # j is outer
  for i in range(3): # i is inner
    c+=B[i][j]*A[i][j] # A[i][j] x B[i][j] 혹은 B[i][j] x A[i][j]
print(c)
## 4. A와 B의 순서 바뀜
c=0.
for i in range(3): # i is outer
  for j in range(3): # j is inner
    c+=B[i][j]*A[i][j] # A[i][j] x B[i][j] 혹은 B[i][j] x A[i][j]
print(c)

NumPy를 활용해서 표현해보자. 아래 두 경우중에 더욱 마음에 드는 스타일이 있는가? 교수자는 개인적으로 후자의 스타일이 더 간략하면서도 직관적이라 마음에 든다.

A=np.array([[1,2,3],[4,5,6],[7,8,9]])
B=np.array([[3,2,1],[6,5,4],[9,8,7]])
##
c=0.
for i in range(3): # i is outer
  for j in range(3): # j is inner
    c+=A[i,j]*B[i,j]

A=np.array([[1,2,3],[4,5,6],[7,8,9]])
B=np.array([[3,2,1],[6,5,4],[9,8,7]])
c=np.einsum('ij,ij->',A,B)

예시

행렬의 축이 늘어나면 늘어날 수록, 정답 예시1과 같은 형태의 코드 스타일은 선호되지 않을 것이다. 여러 인공지능 기술에서 매우 차원이 높은 다수의 행렬들간의 복잡한 연산이 요구된다. 그럴 경우, Einstein summation 기법을 익히고 간략히 표현할 수 있을수록 유리할 것이다.









Week6

수업 06-1 (Eigenvalue)

06-1-1 개념

06-1-2 선형 변환(linear transformation; linear map)

06-1-2-1 선형변환 조건

<img src=https://upload.wikimedia.org/wikipedia/commons/4/43/Streckung_eines_Vektors.gif />

<img src=https://upload.wikimedia.org/wikipedia/commons/2/25/Streckung_der_Summe_zweier_Vektoren.gif />

<img src=https://upload.wikimedia.org/wikipedia/commons/e/e6/Streckung_homogenitaet_Version_3.gif />

** Wikipedia 발췌 이미지

06-1-2-2 선형변환 특성

06-1-3

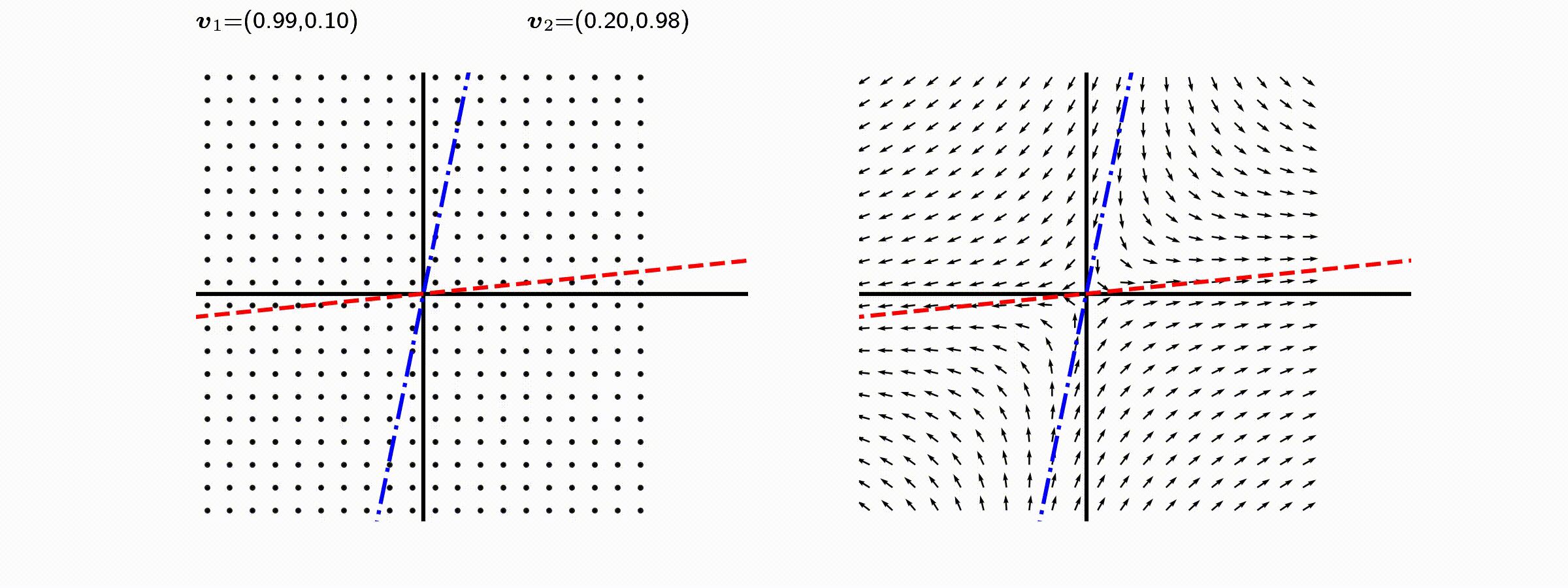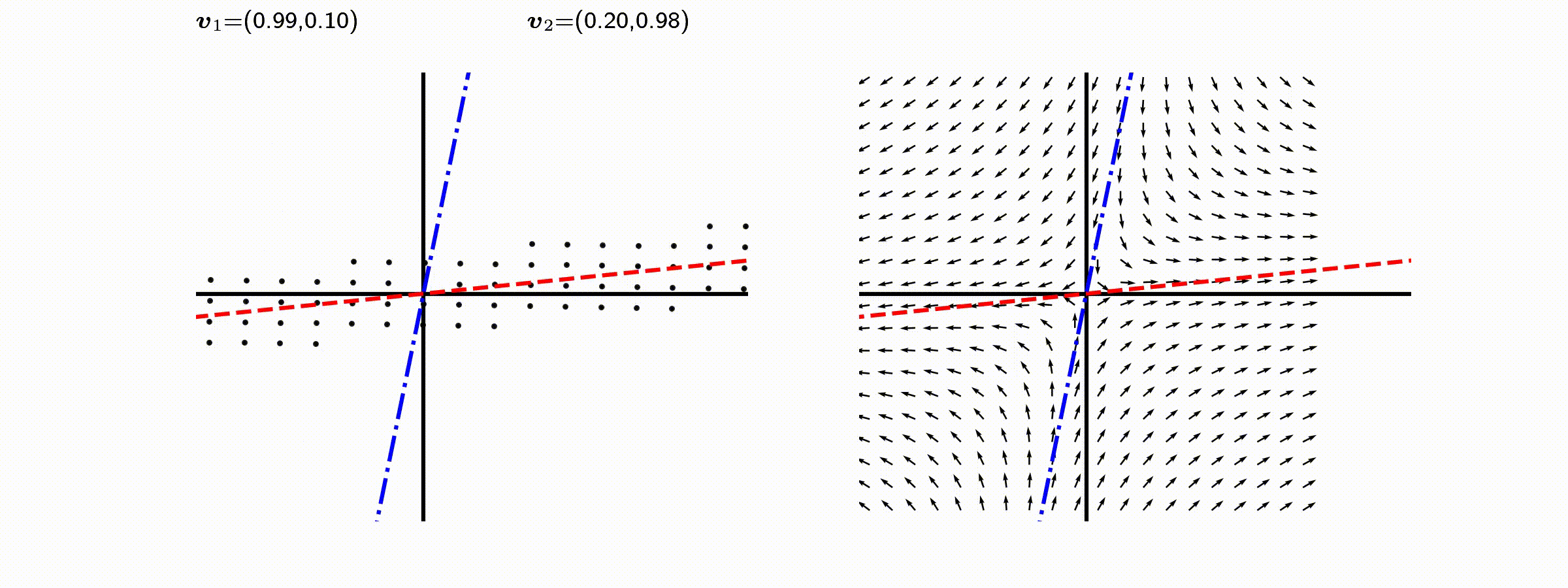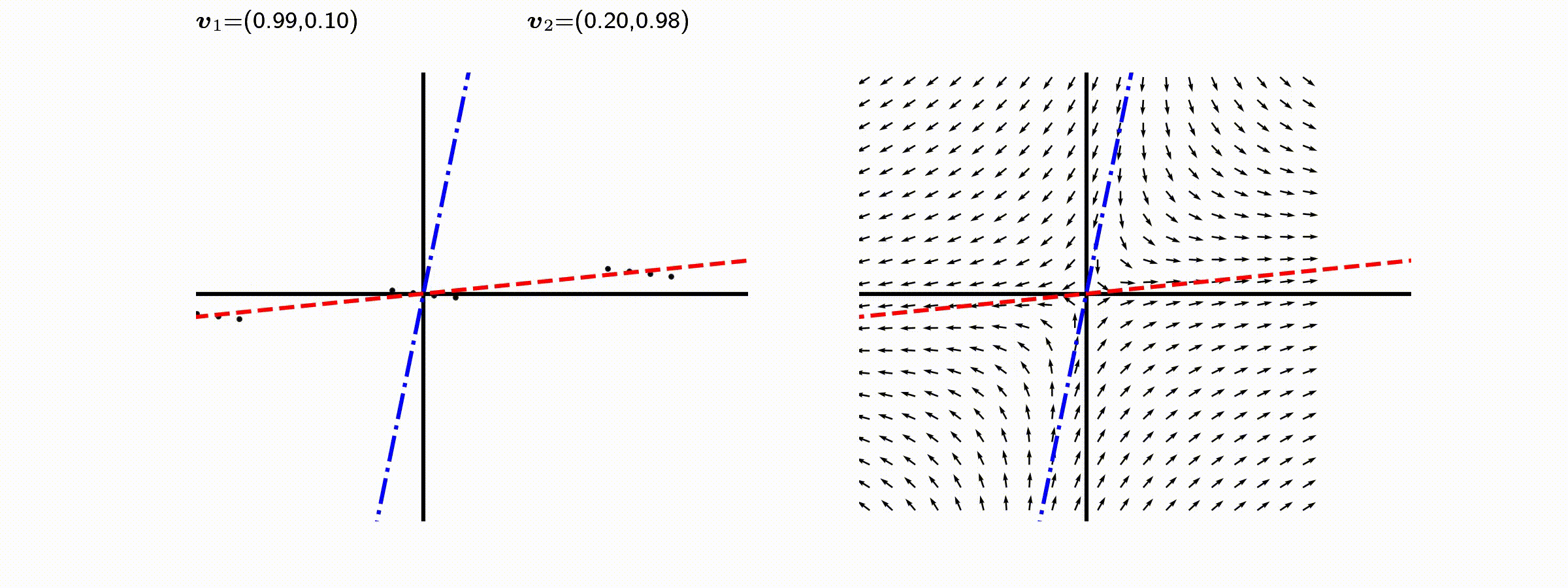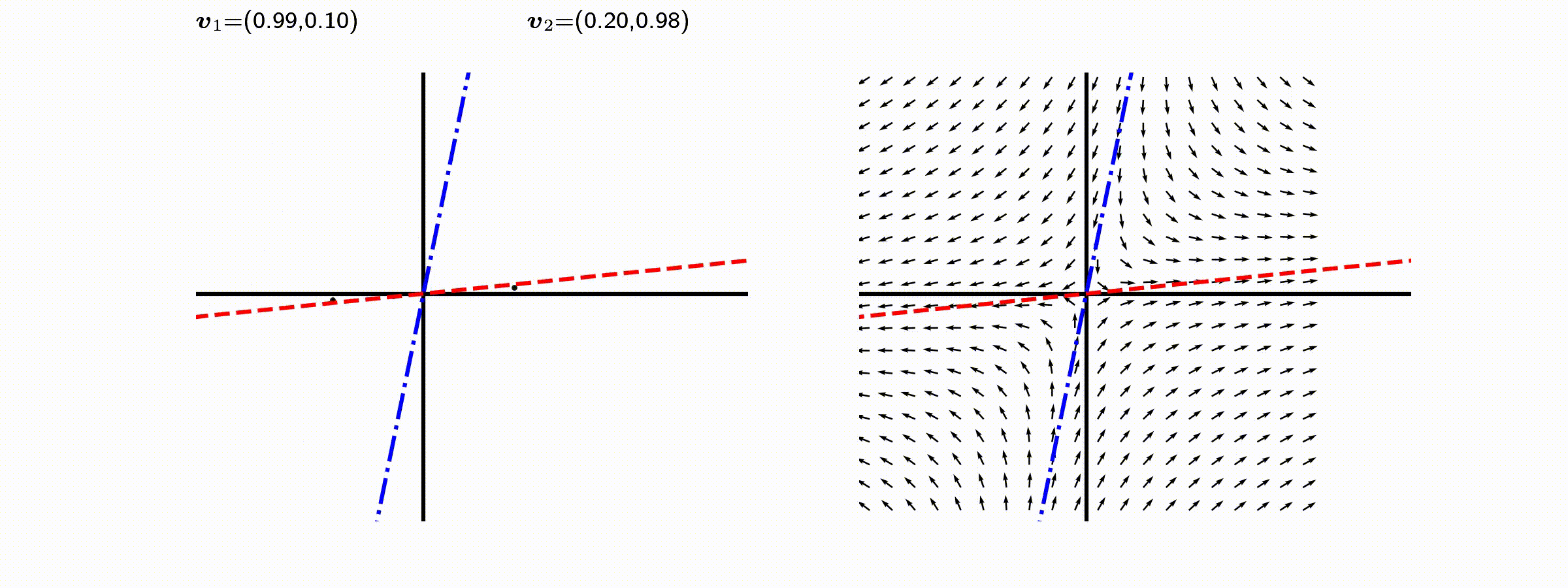
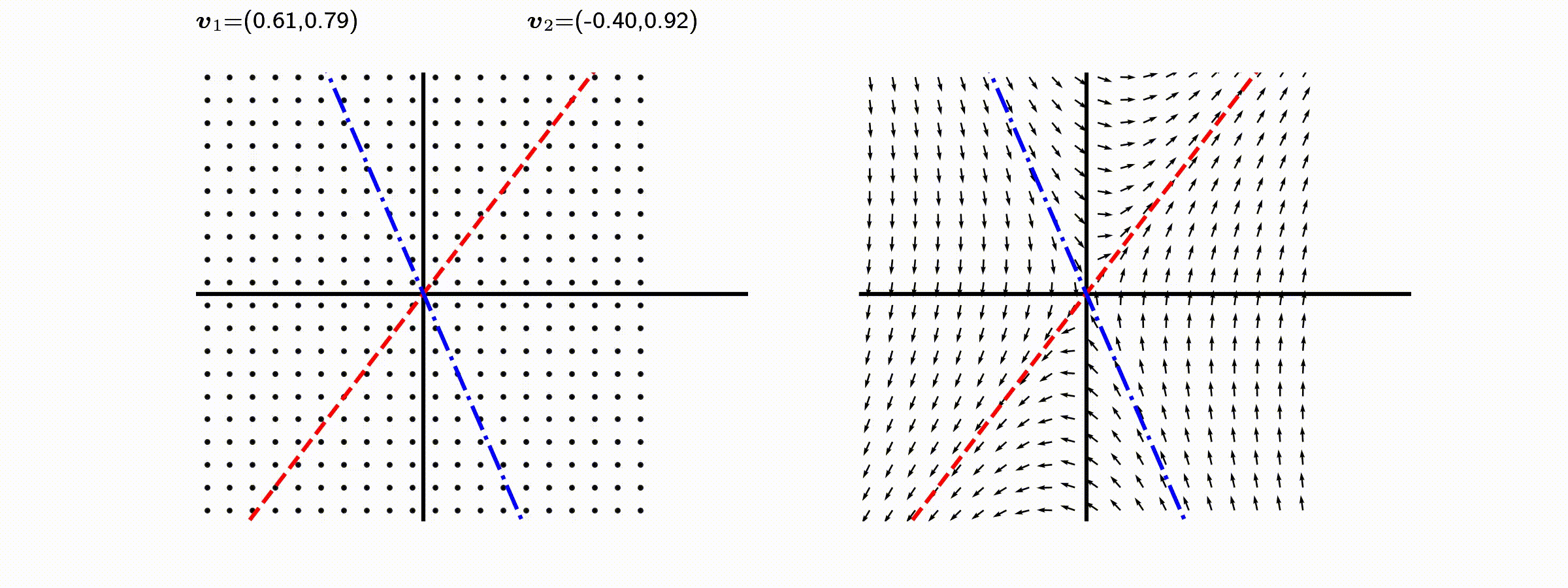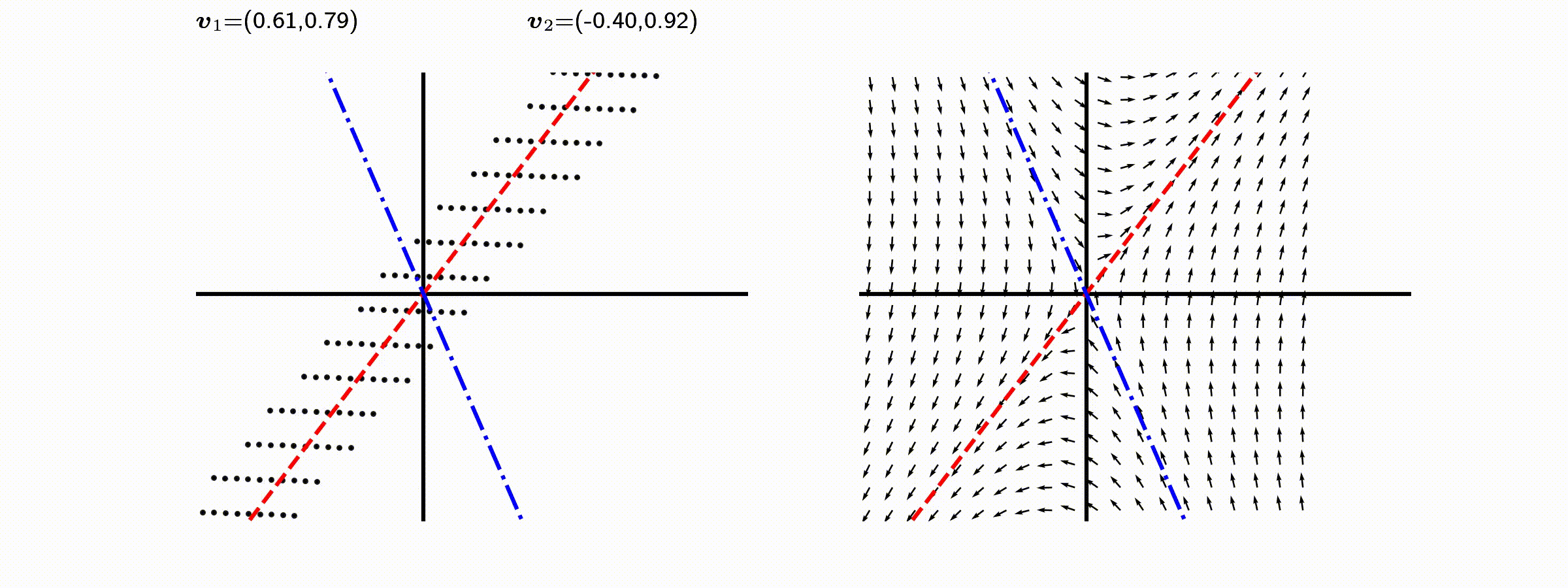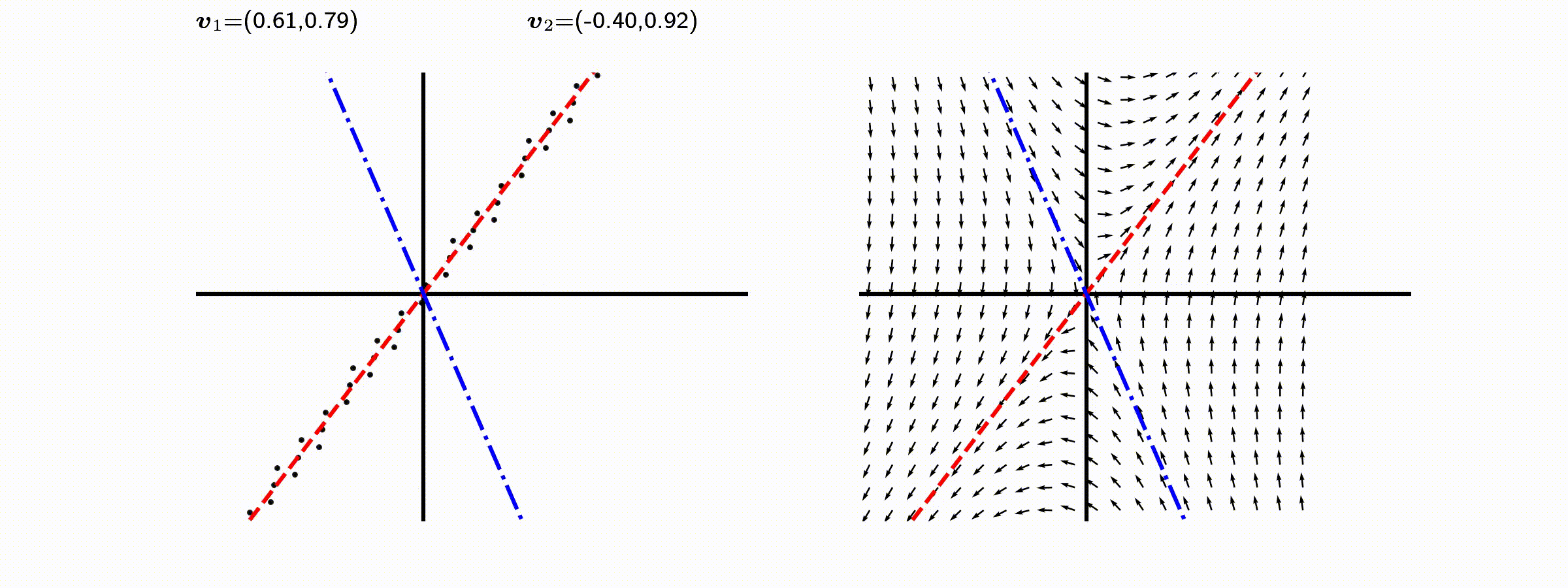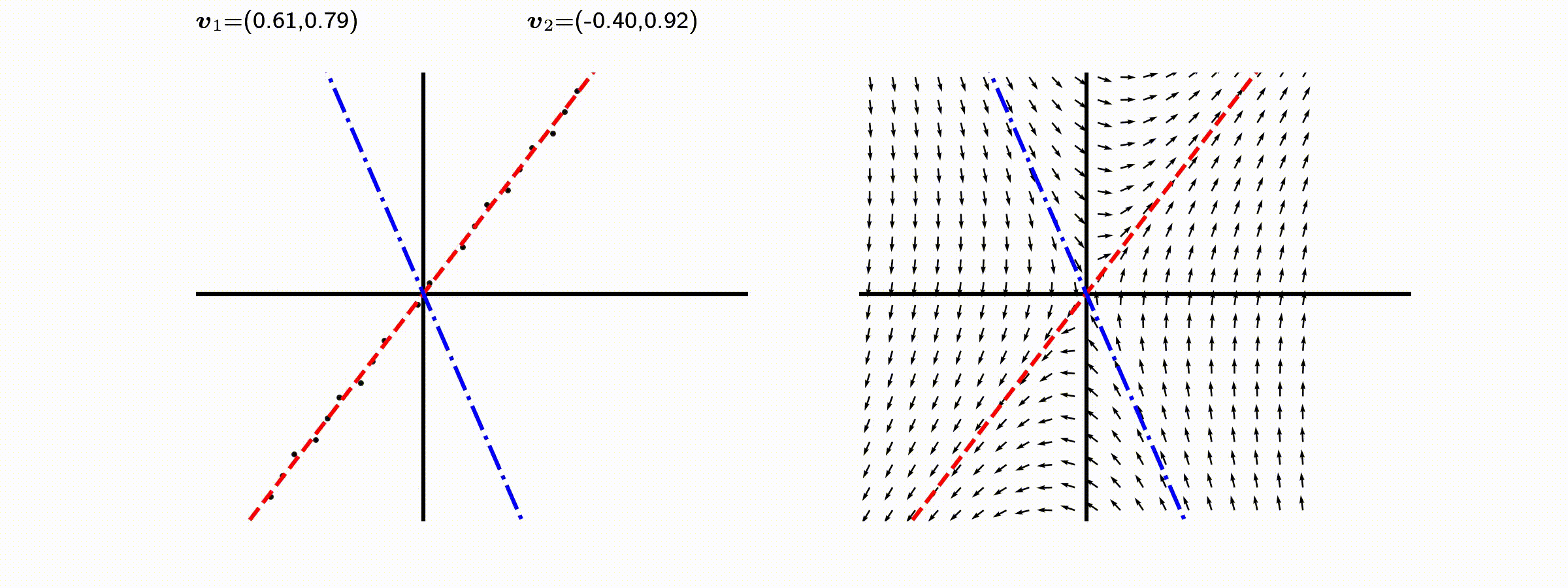
고유값의 기하학적 의미를 파악해보자. 다음과 같은 행렬의 경우를 살펴보자. 다음의 여러 행렬들에 의한 벡터(점)의 변환을 살펴보자. 그리고 빨간 선과 (표기되어 있다면) 파란 선 위의 점들이 다른 점들과 어떠한 차이가 있는지 눈여겨 살펴보자.

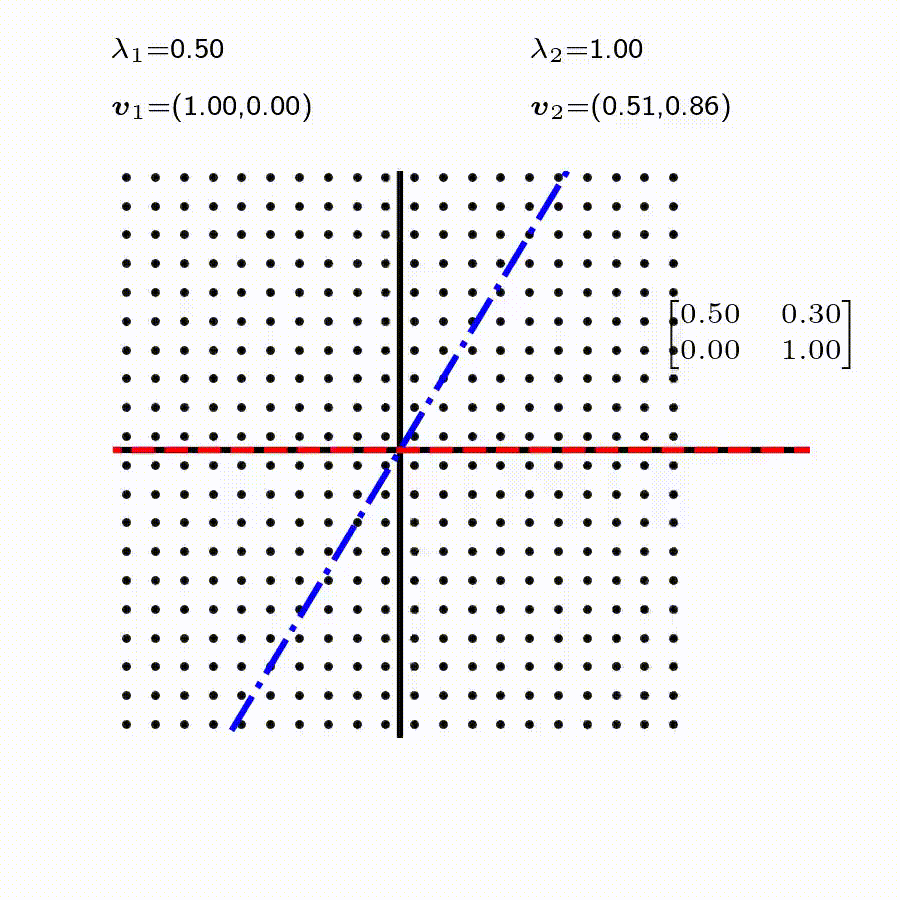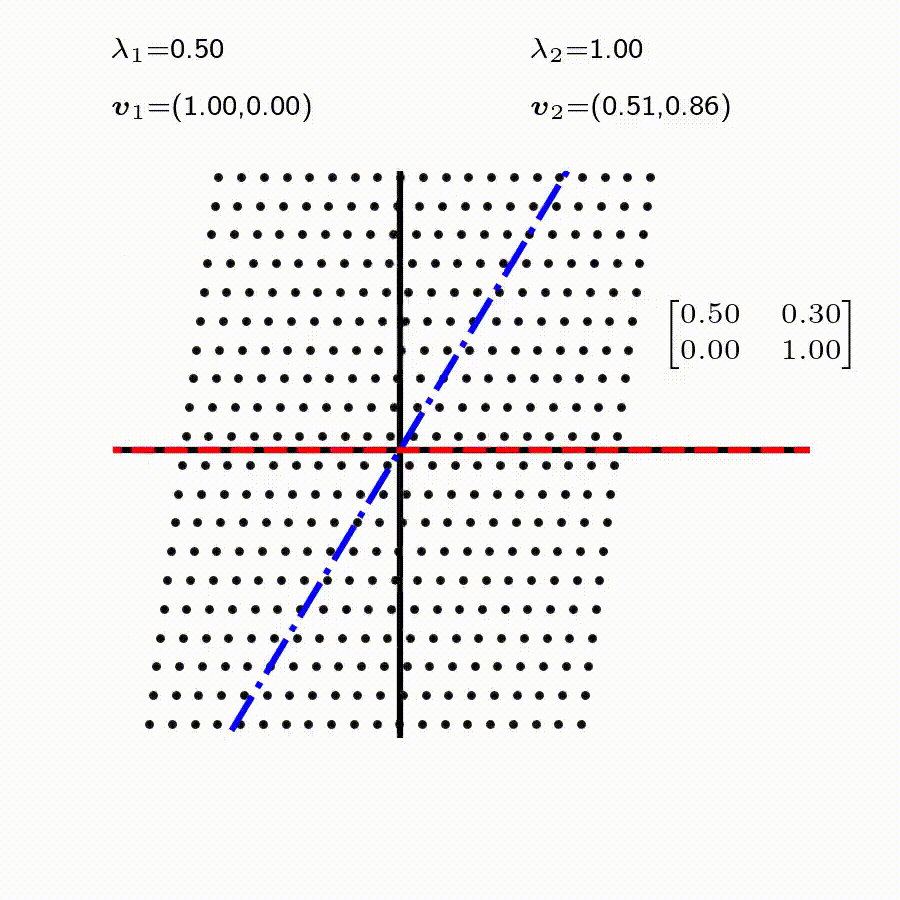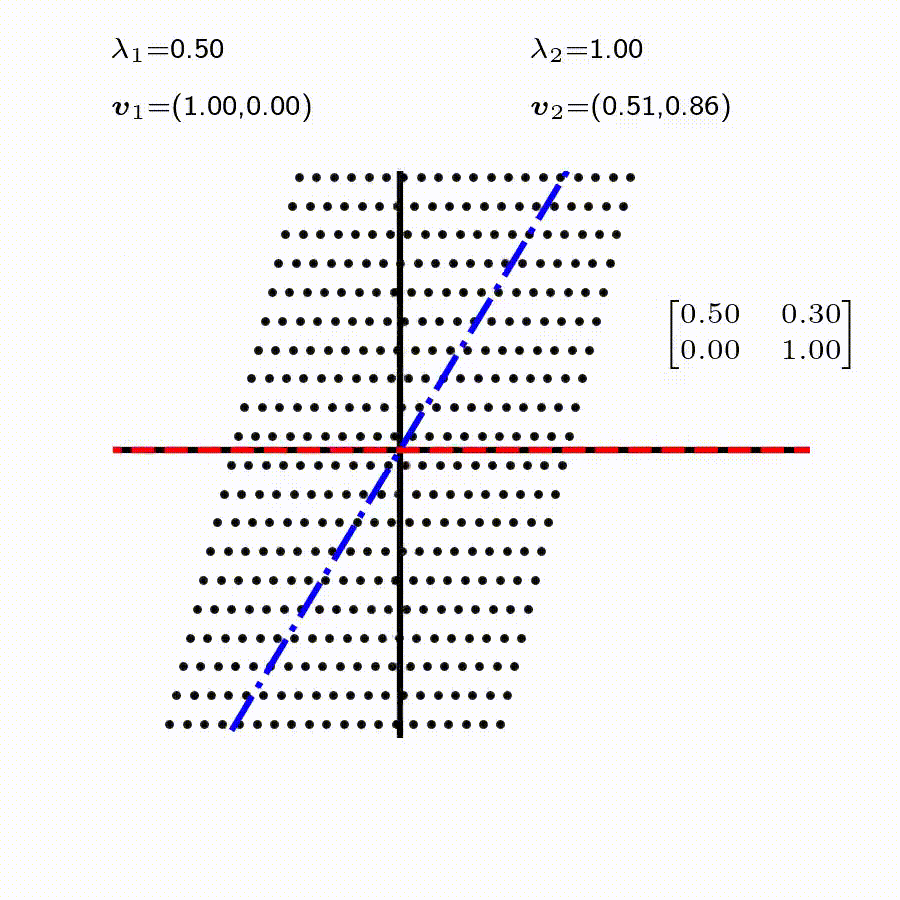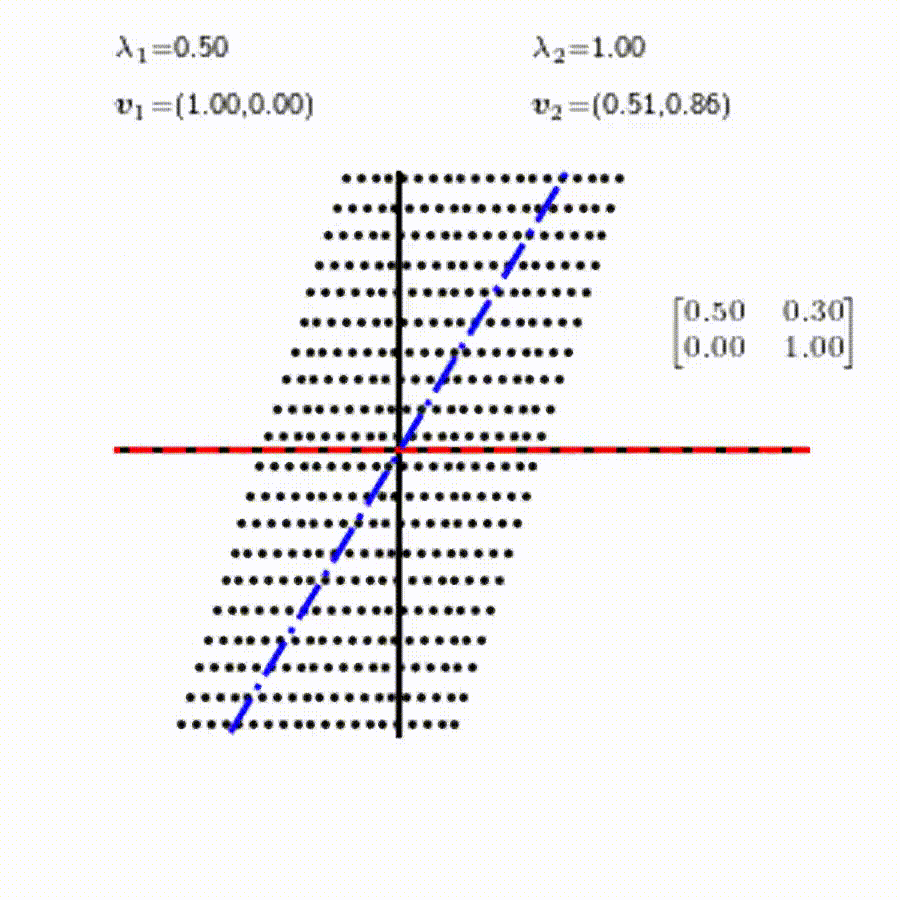
eigen1

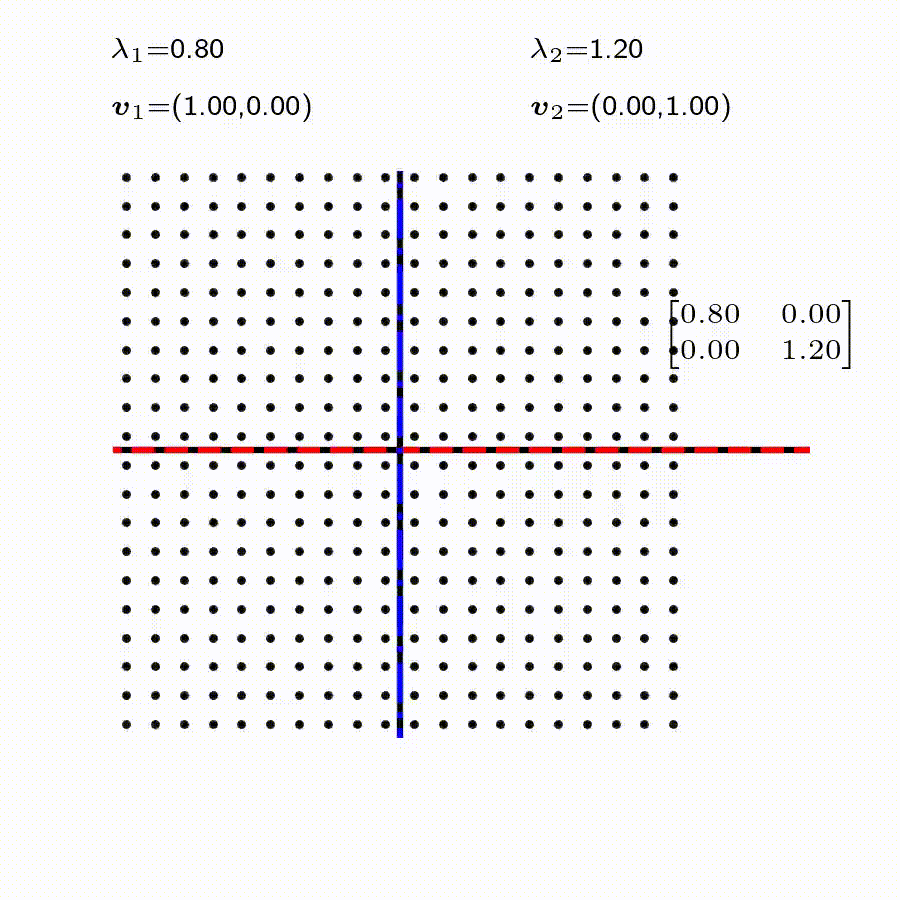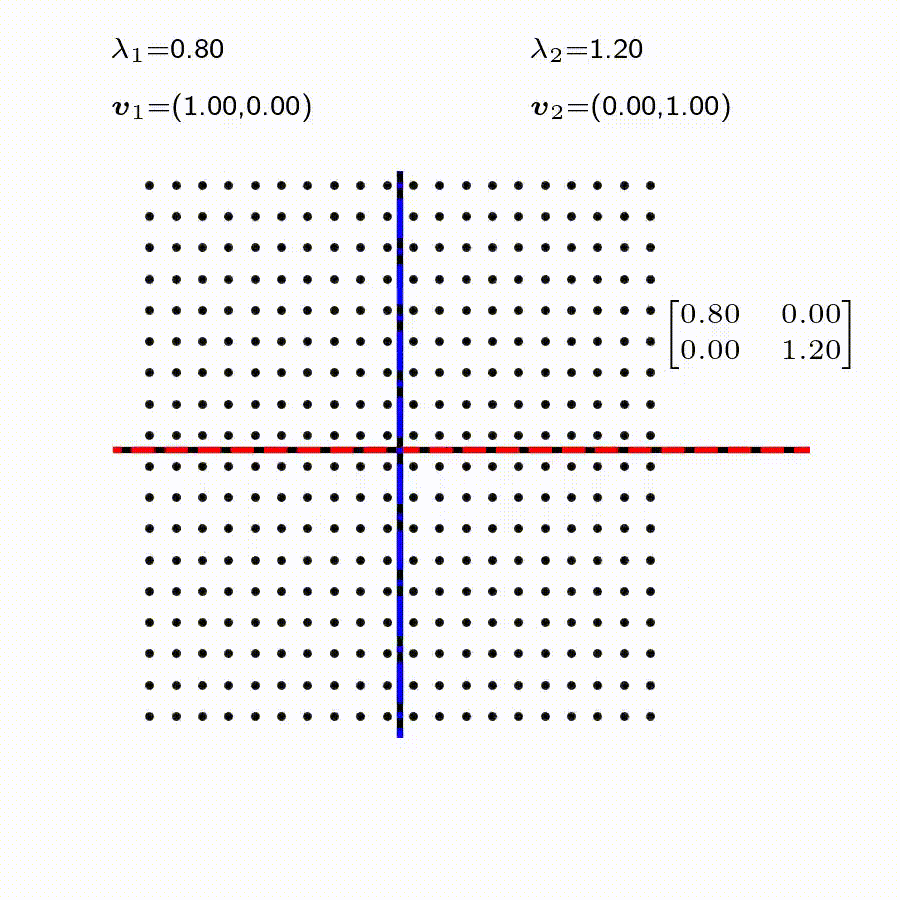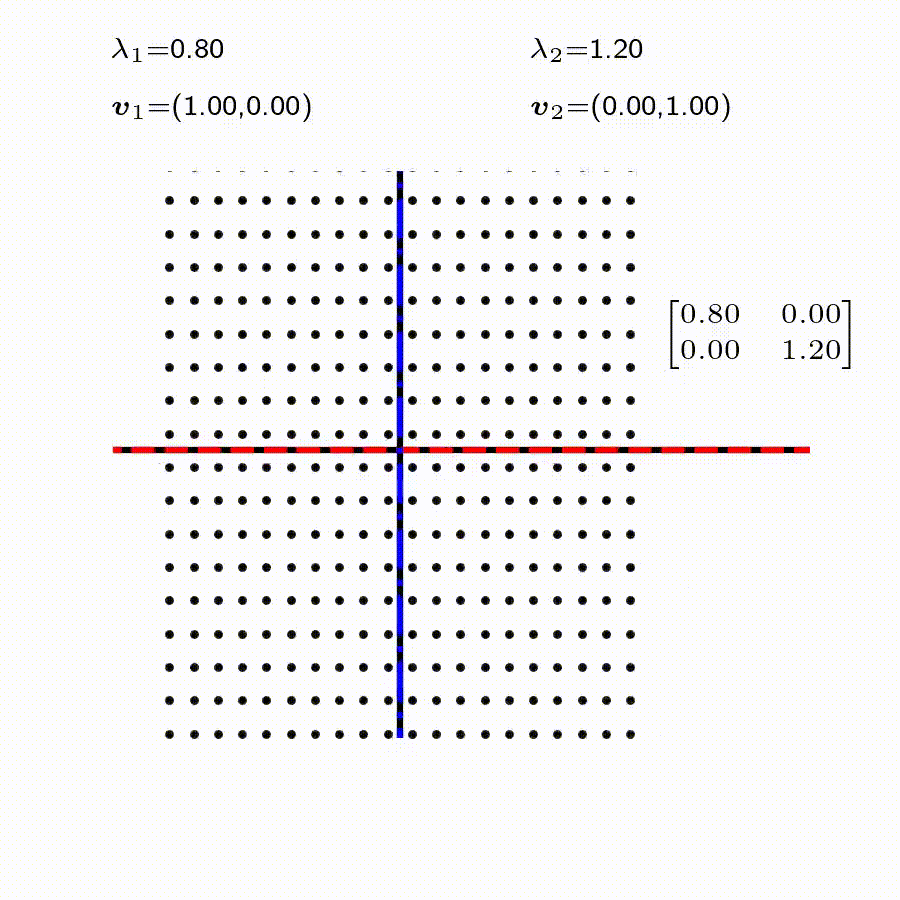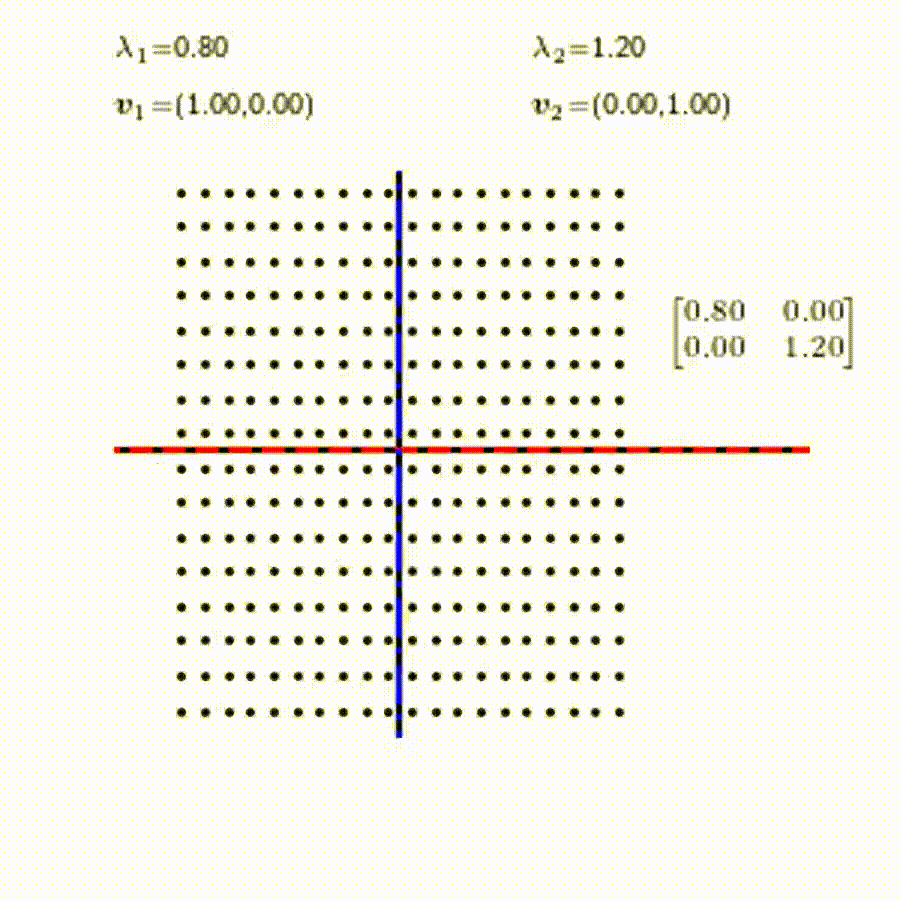
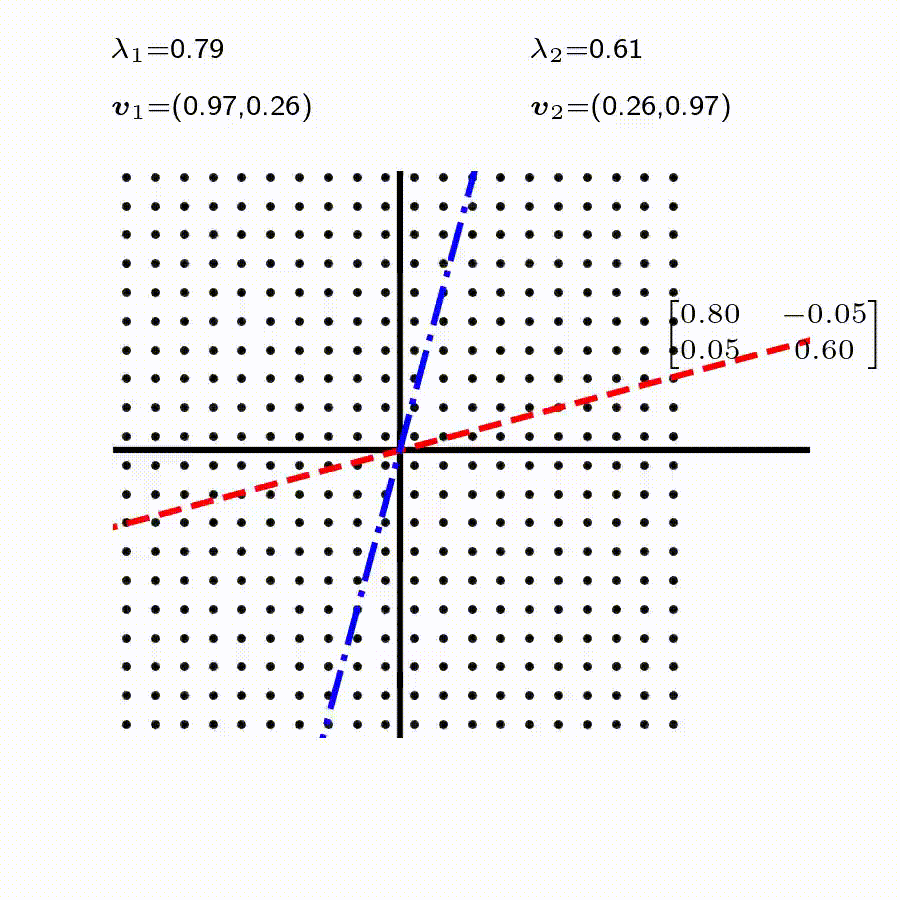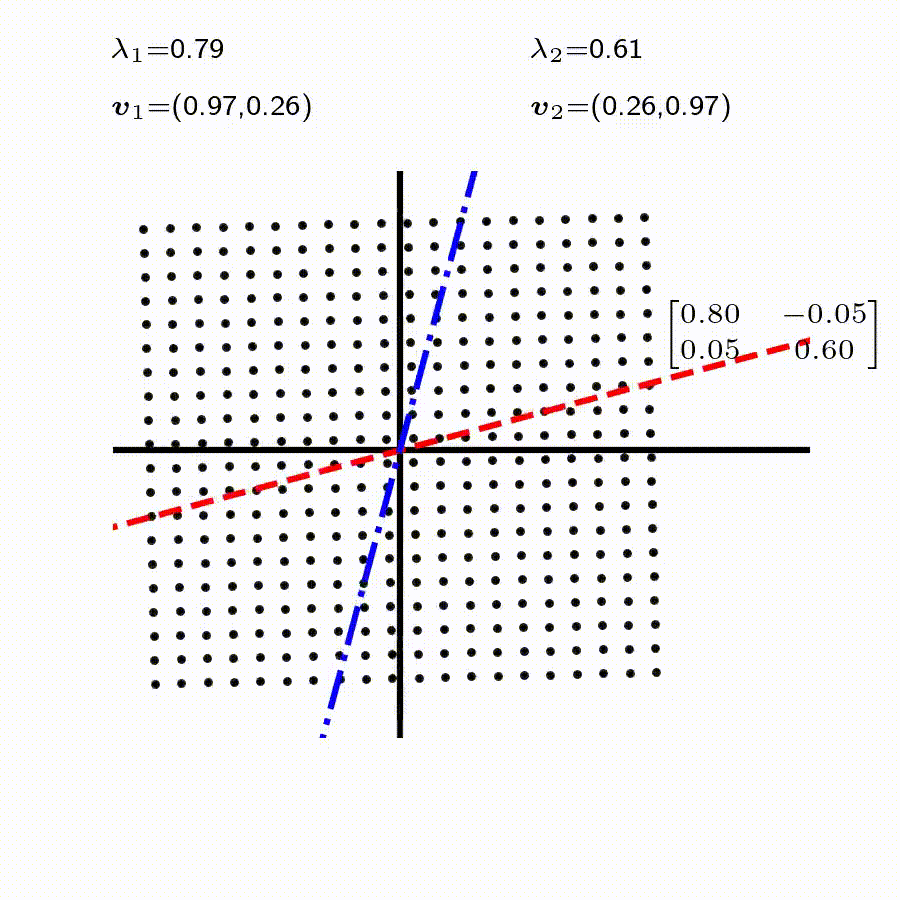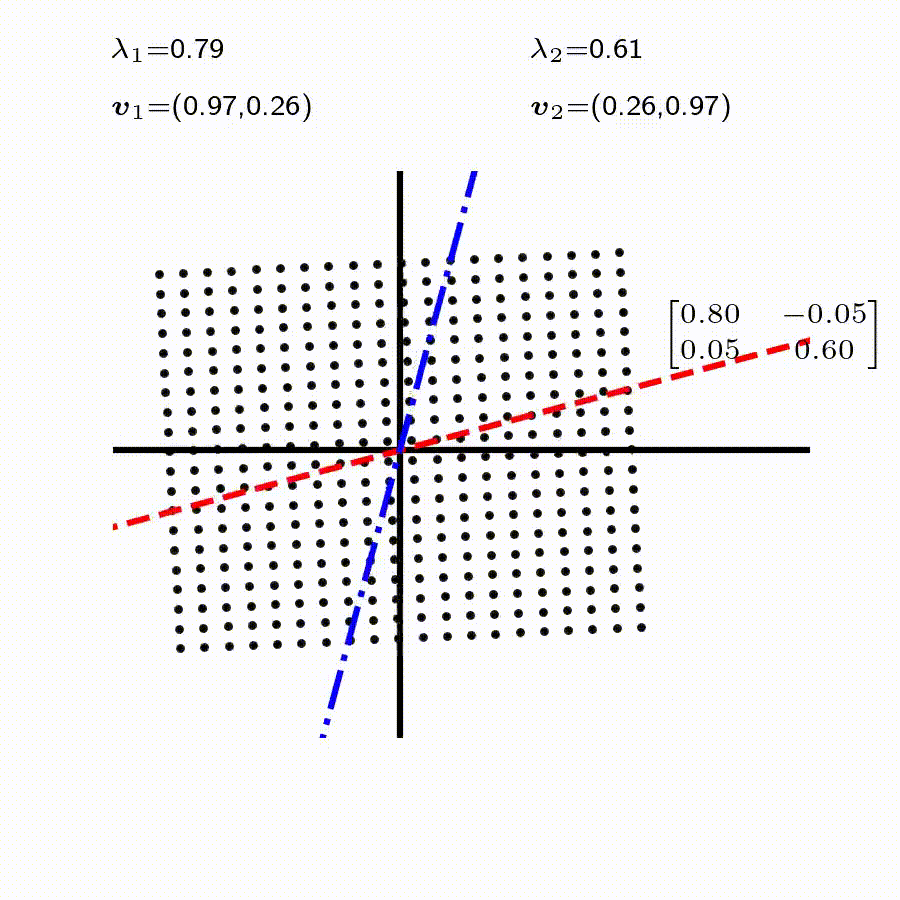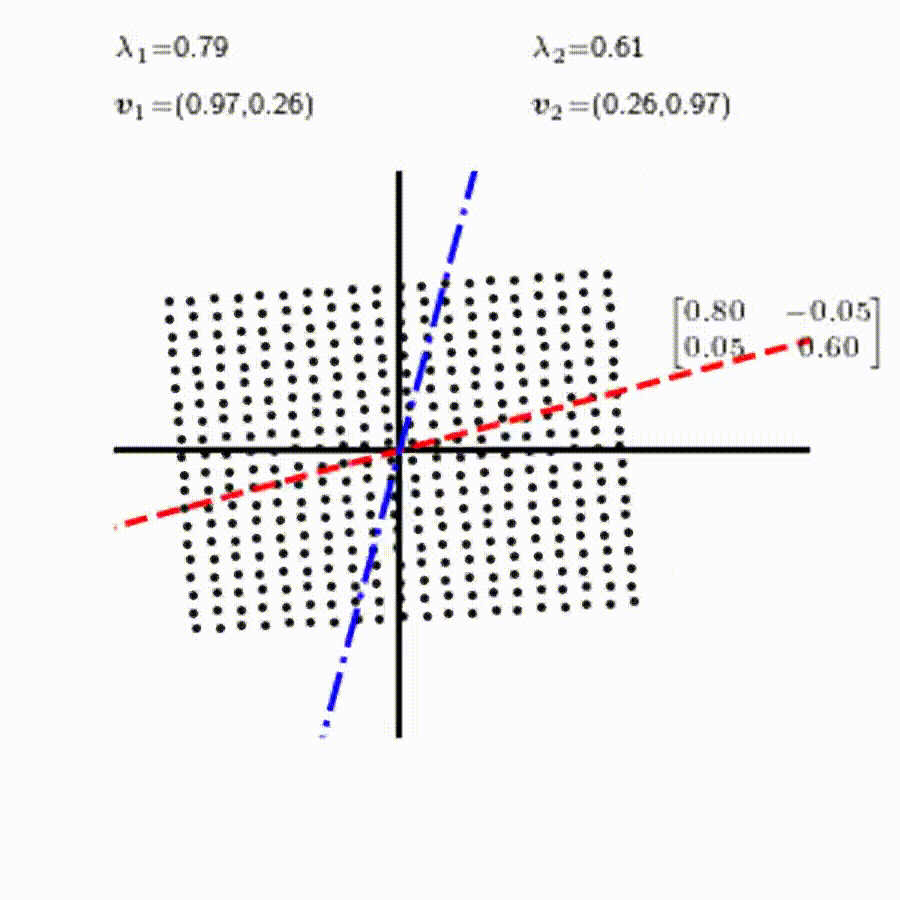
eigen2

eigen2

위 세 경우와 달리, 아래 경우는 조금 특별하다. 특성값이 복소수 \(\lambda_1=0.71+0.71i,\) 그리고 \(\lambda_2=0.71-0.71i\) 임을 눈여겨 보자.

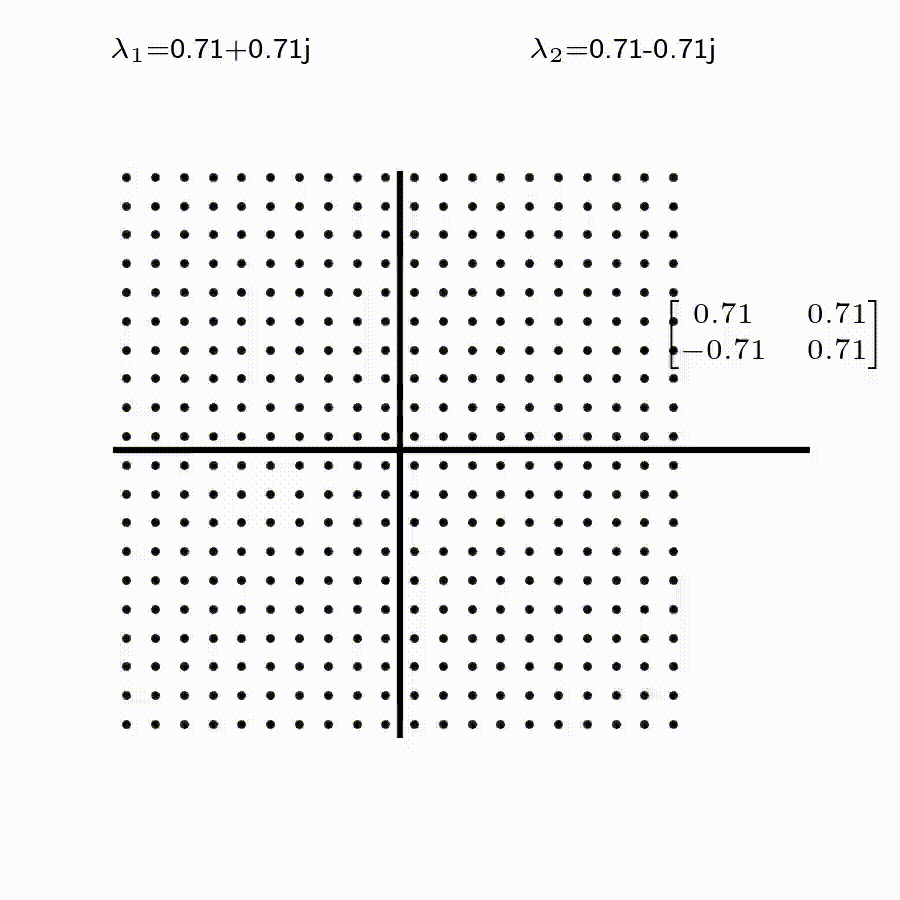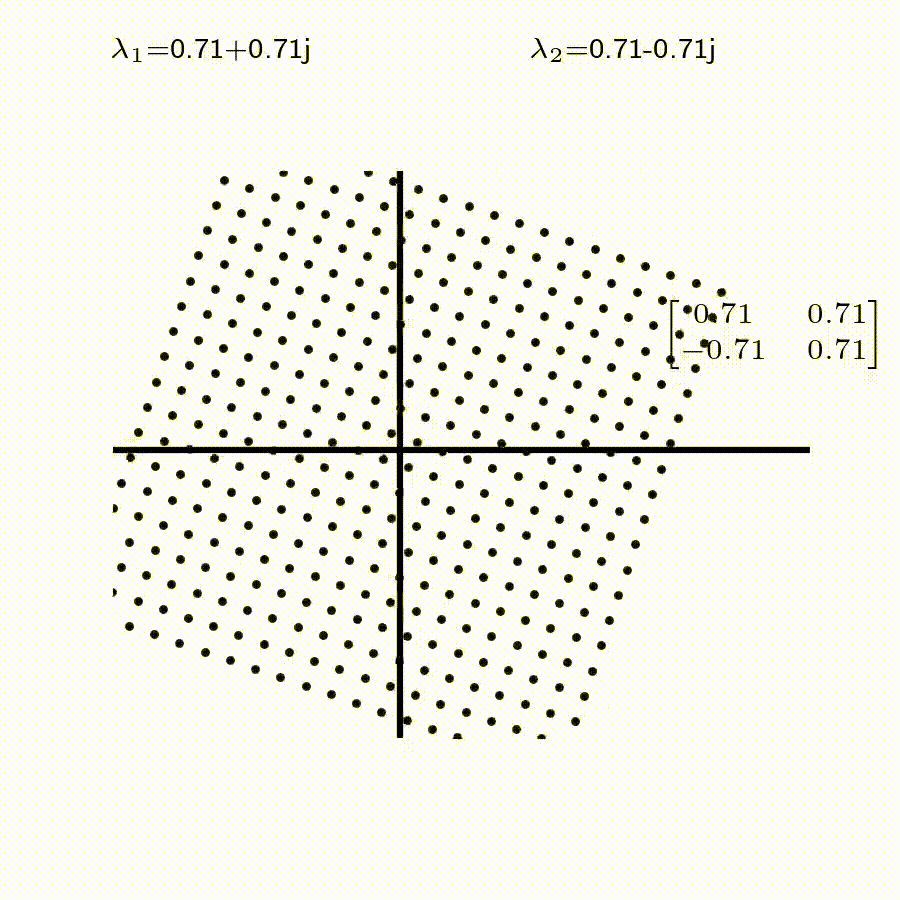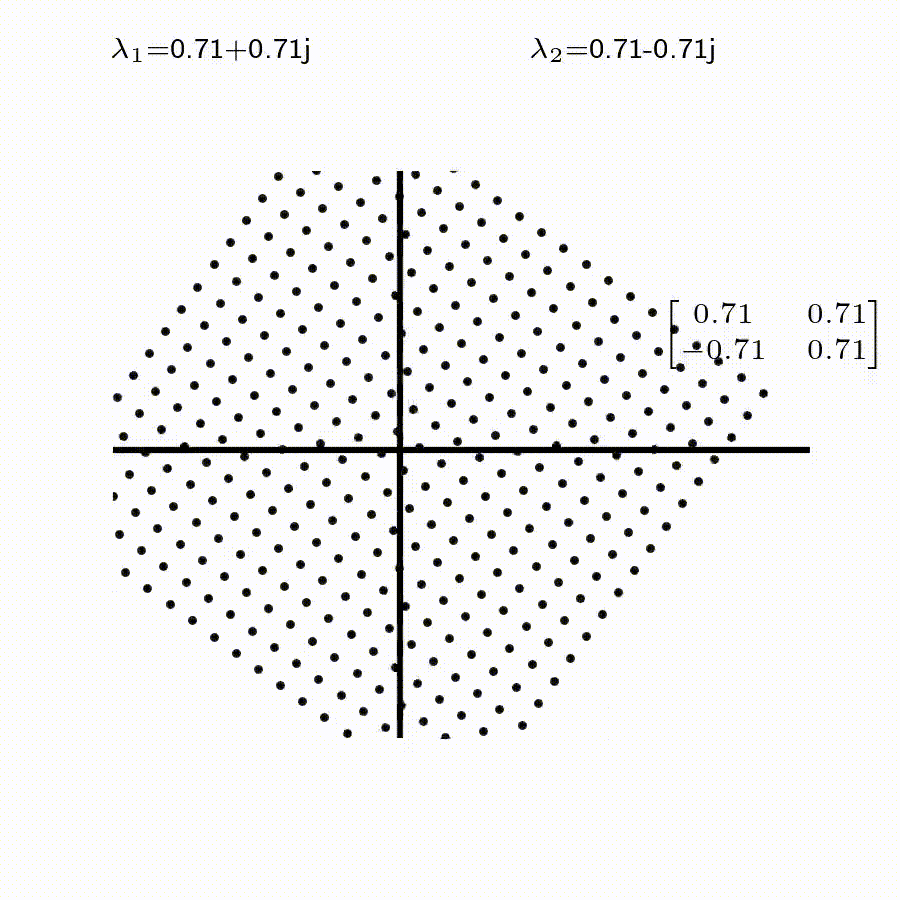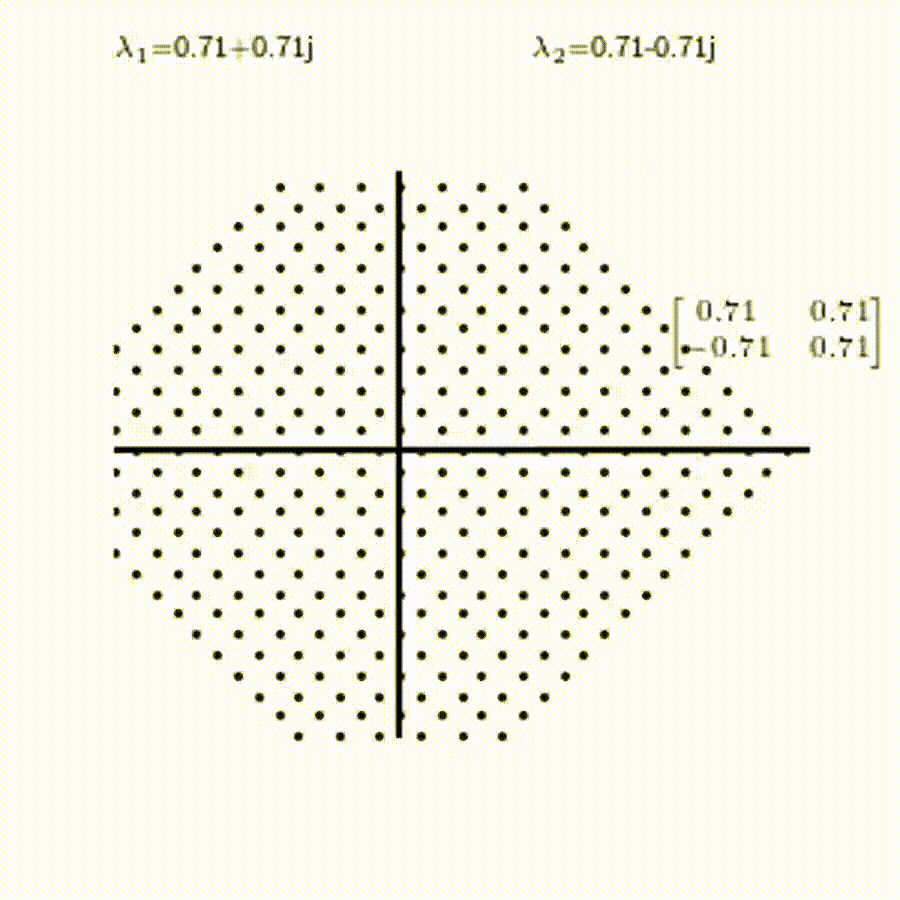
eigen3

06-1-4 Eigenvalue, Eigenvector 구하기.

역학에서 변위구배텐서(displacement gradient tensor) $\boldsymbol u$라는 물리량을 활용해, 변형 전 후의 위치변화를 다음과 같이 위치를 나타내는 벡터 변환으로 나타낸다.

\[\boldsymbol v^{new}=\boldsymbol u \cdot \boldsymbol v^{old}\]

이때, 변위구배텐서의 eigen value를 활용해 변형의 량을 가늠해볼 수 있다. 2차원 변위구배텐서의 특성값을 각각 $\lambda_1, \lambda_2$라 한다면, 경우에 따라 (회전이 거의 없다면) $\lambda_1-1$과 $\lambda_2-1$은 꽤 괜찮은 변형의 정도를 나타내는 지표가 될 수 있다. 여기서 1을 빼는 이유는 무엇일까?

신분제가 공고하던 조선 시대에서도 양반과 노비 계층간의 변화가 일어나곤 했다 (참고). 매우 불안정했던 가상의 조선시대에 매년 역적으로 몰린 양반의 20%가 노비가 되고, 노비 중 10%가 큰 부를 쌓아 양반으로 신분상승을 했다고 가정하자.

stateDiagram-v2

Yangban(YB) --> Nobi(NB) : 20%
Nobi(NB) --> Yangban(YB): 10%

해가 거듭 될 수록 달라지는 양반(YB)과 노비(NB)의 상관 관계를 수식으로 표현하자면 아래와 같다. \(YB_{(n+1)} = 0.80 YB_{(n)} + 0.10 NB_{(n)}\) \(NB_{(n+1)} = 0.20 YB_{(n)} + 0.90 NB_{(n)}\) 여기서 첨자 ${n}$과 ${n+1}$은 각각 직전 해, 그리고 다음해에 해당하는 노비와 양반을 가리킨다. 위 연립 방정식을 아래와 같이 행렬식으로 나타낼 수 있겠다. $$ \begin{bmatrix} YB_{(n+1)}
NB_{(n+1)} \end{bmatrix} = \begin{bmatrix} 0.90& 0.01
0.02& 0.95 \end{bmatrix}

\begin{bmatrix} YB_{(n)}
NB_{(n)} \end{bmatrix} $$

예들 들어, 양반과 노비의 인구수가 첫해($n=0$)에 8명 vs 2명 이었다고 가정하자. 그 다음해에는 $$ \begin{bmatrix} YB_{(1)}
NB_{(1)} \end{bmatrix} = \begin{bmatrix} 0.8& 0.1
0.2& 0.90 \end{bmatrix}

\begin{bmatrix} 8
2 \end{bmatrix} = \begin{bmatrix} 6.60
3.40 \end{bmatrix} \(그리고 그 다음에는\) \begin{bmatrix} YB_{(2)}
NB_{(2)} \end{bmatrix} = \begin{bmatrix} 0.8& 0.1
0.2& 0.90 \end{bmatrix}

\begin{bmatrix} 6.60
3.40 \end{bmatrix} = \begin{bmatrix} 5.62
4.38 \end{bmatrix} $$

이렇게 차례로 시간이 더욱 지나고 나면 3.34, 6.66으로 수렴된다. 하지만 초기 세팅이 8대2가 아니라 8대 4였다면 4대 8로 바뀌게 된다. 위 경우를 포함해 양반대 노비의 비율이 각기 다를경우에도 시간이 충분히 지나면, 규칙성 있게 바뀌게 된다. 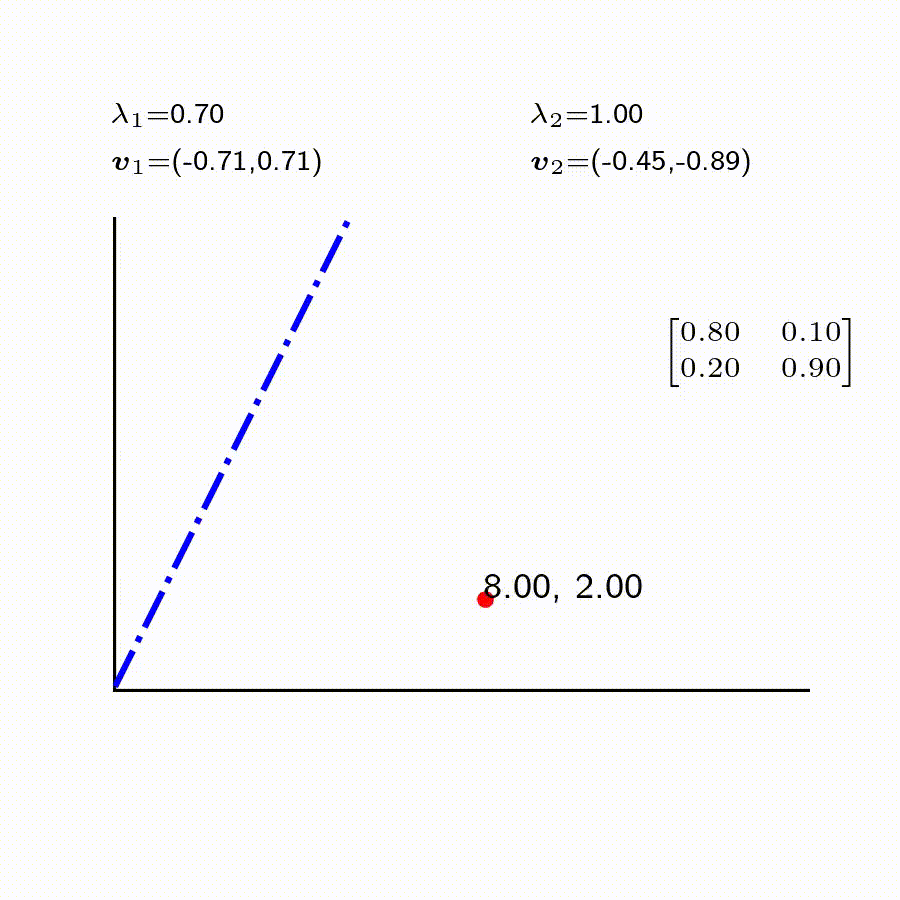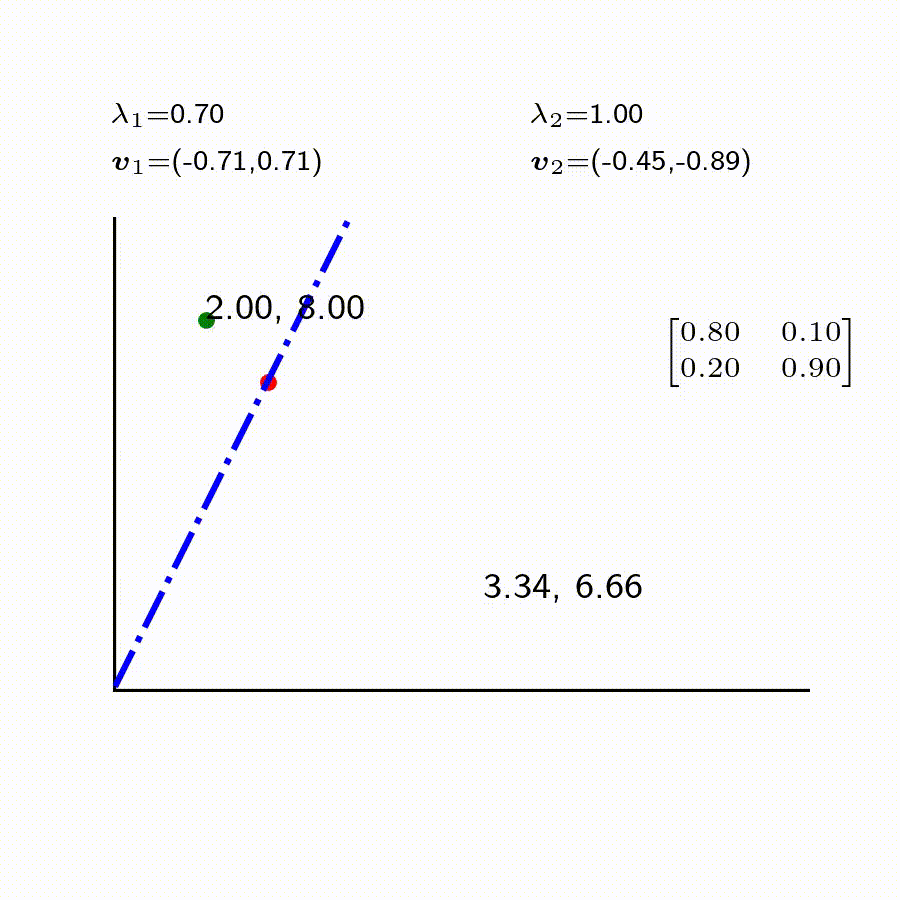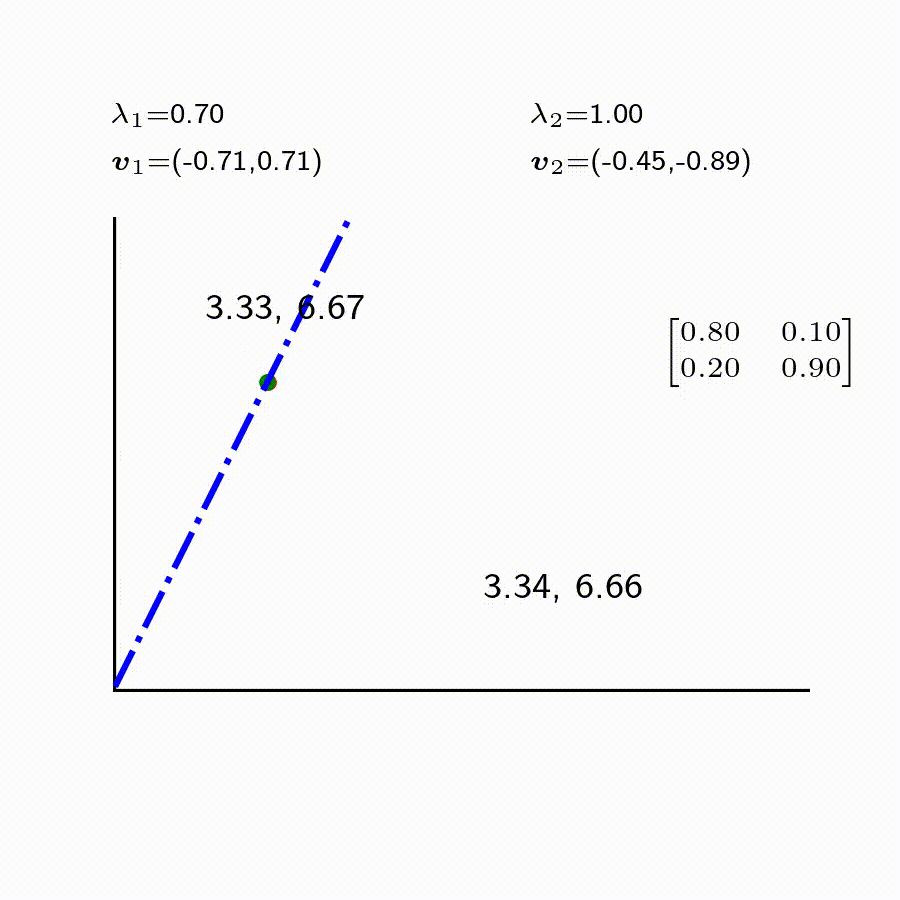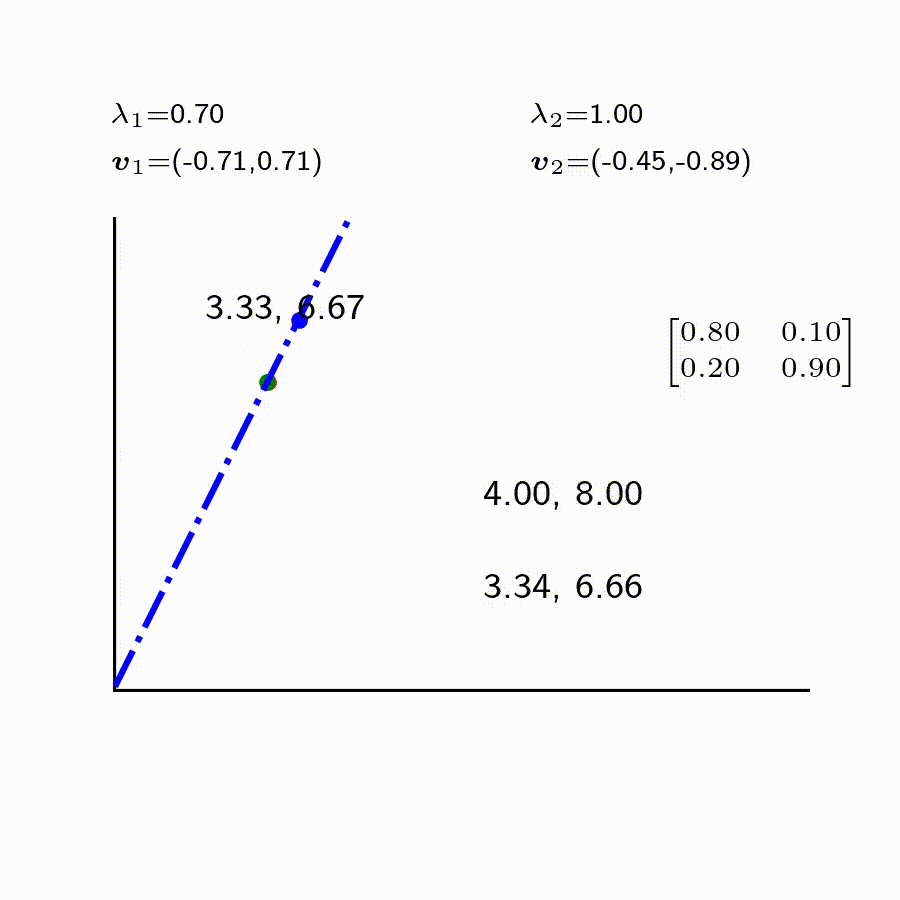NBYB

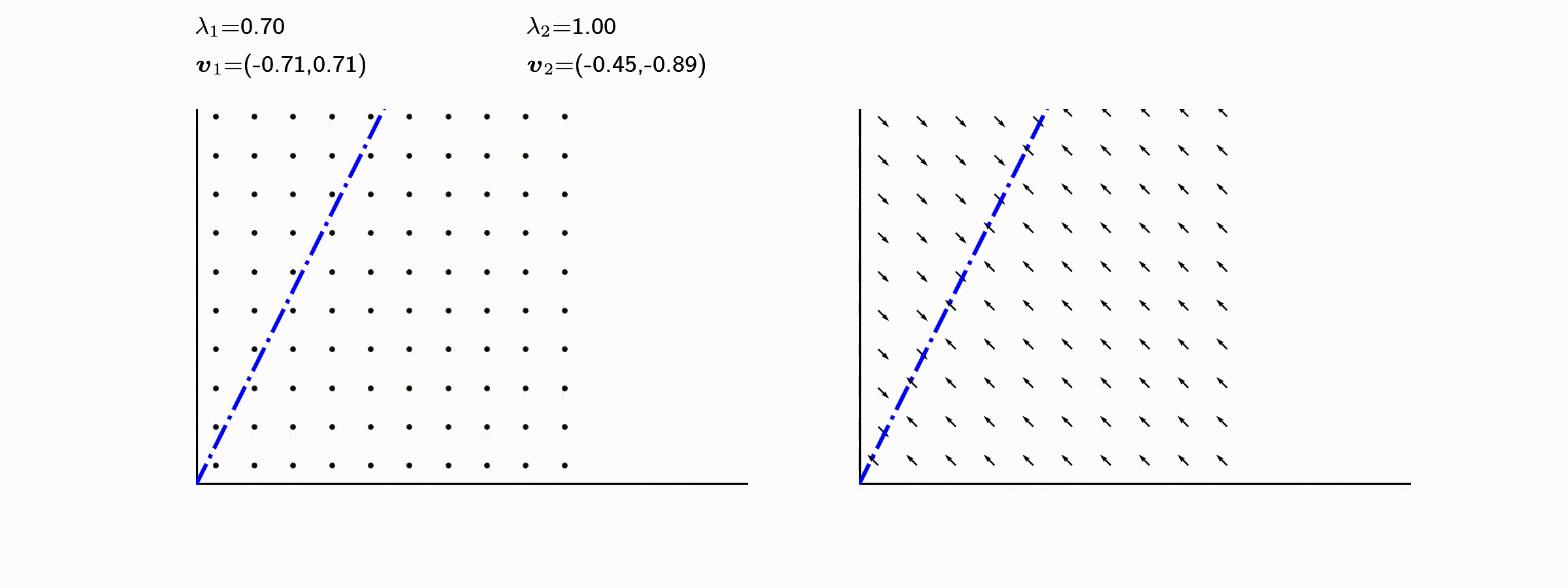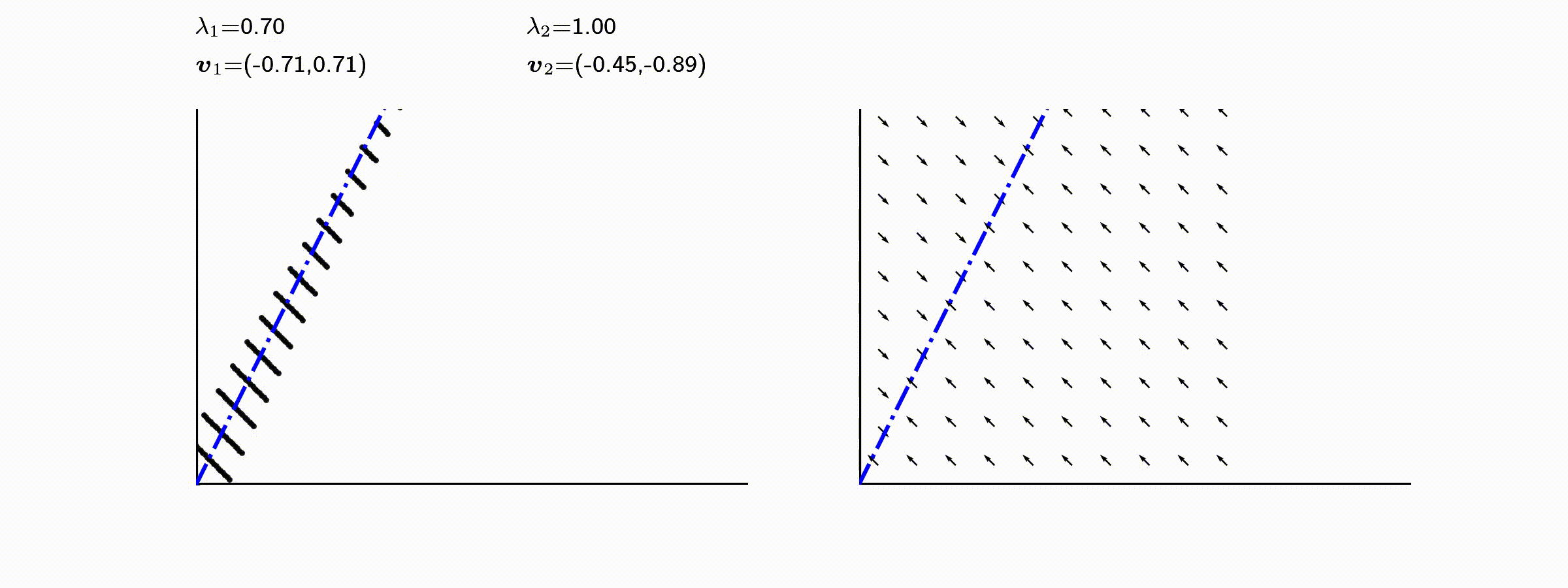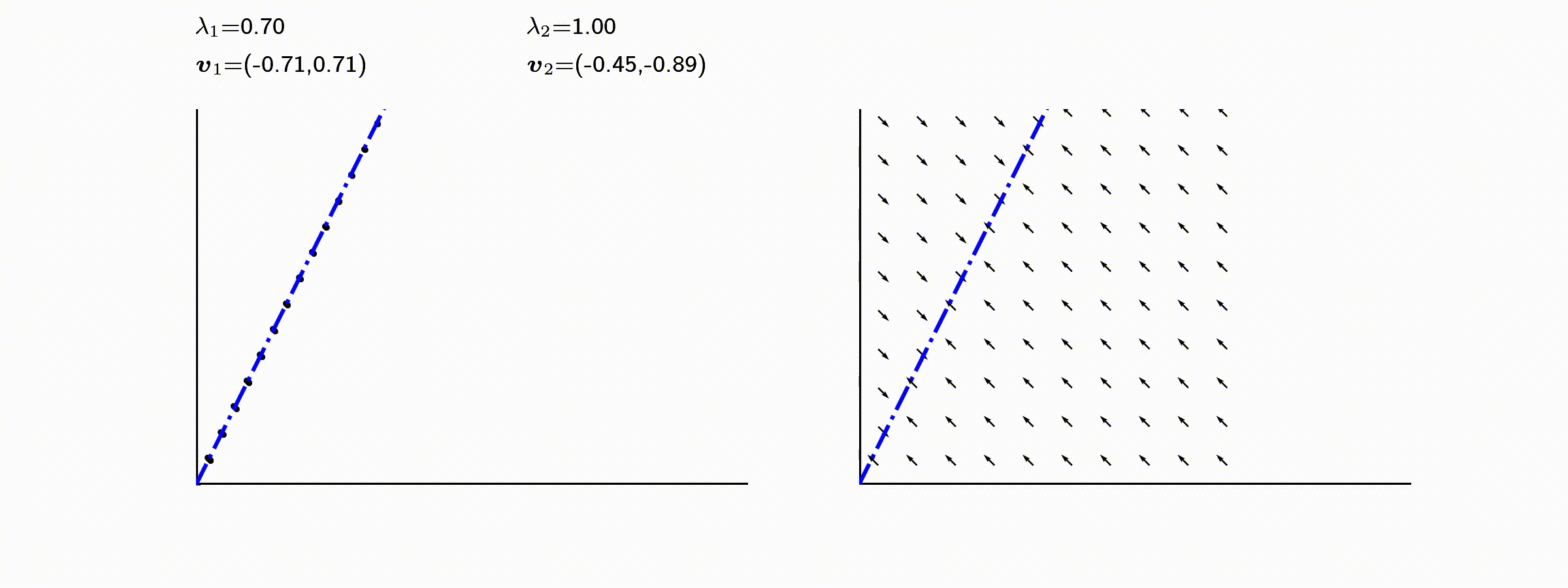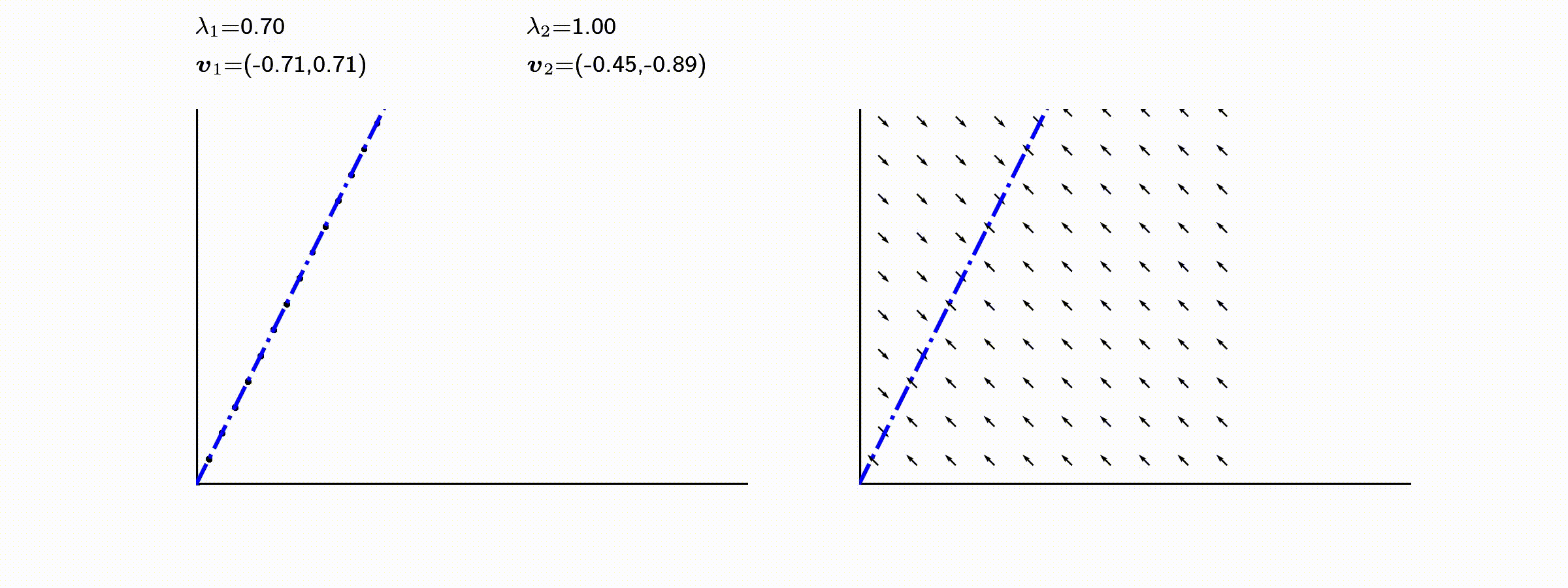
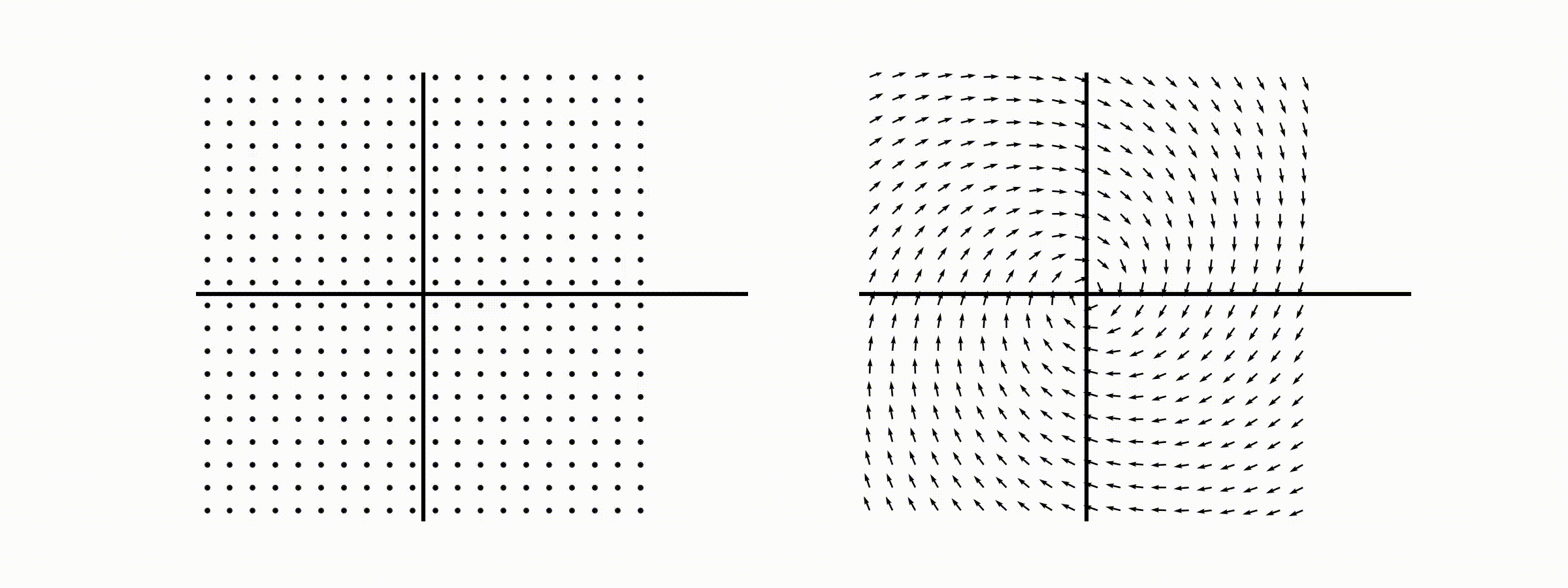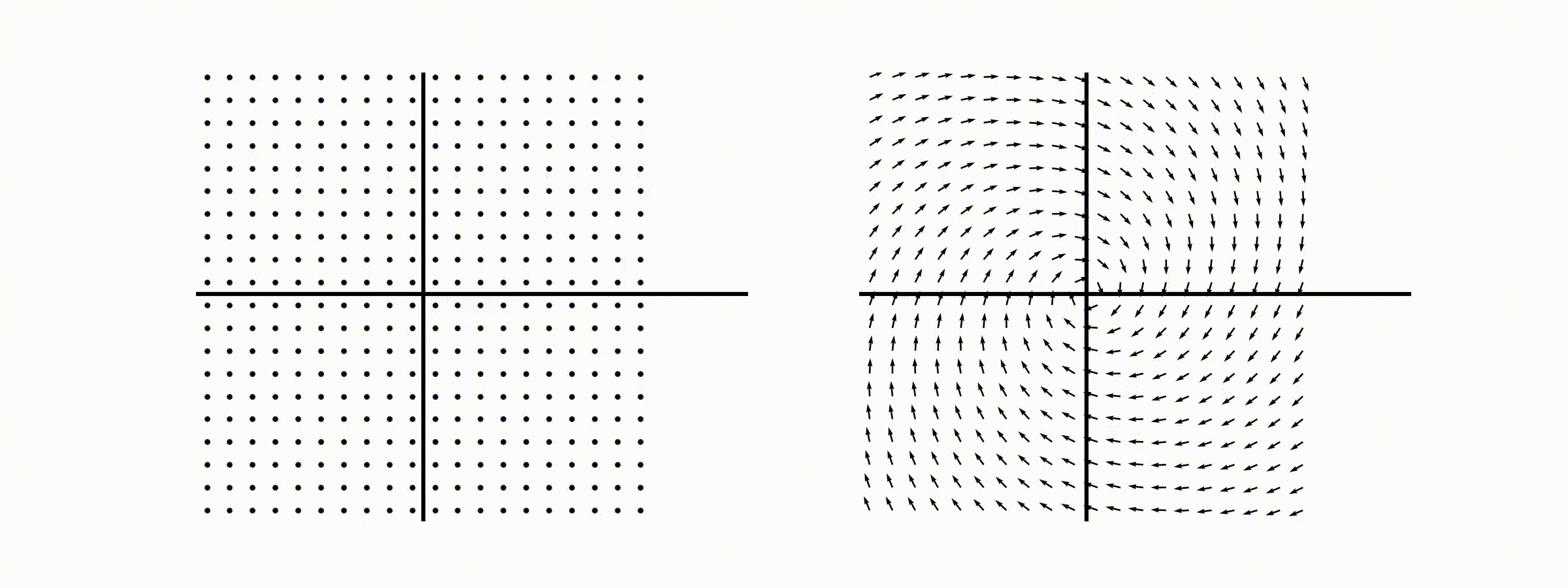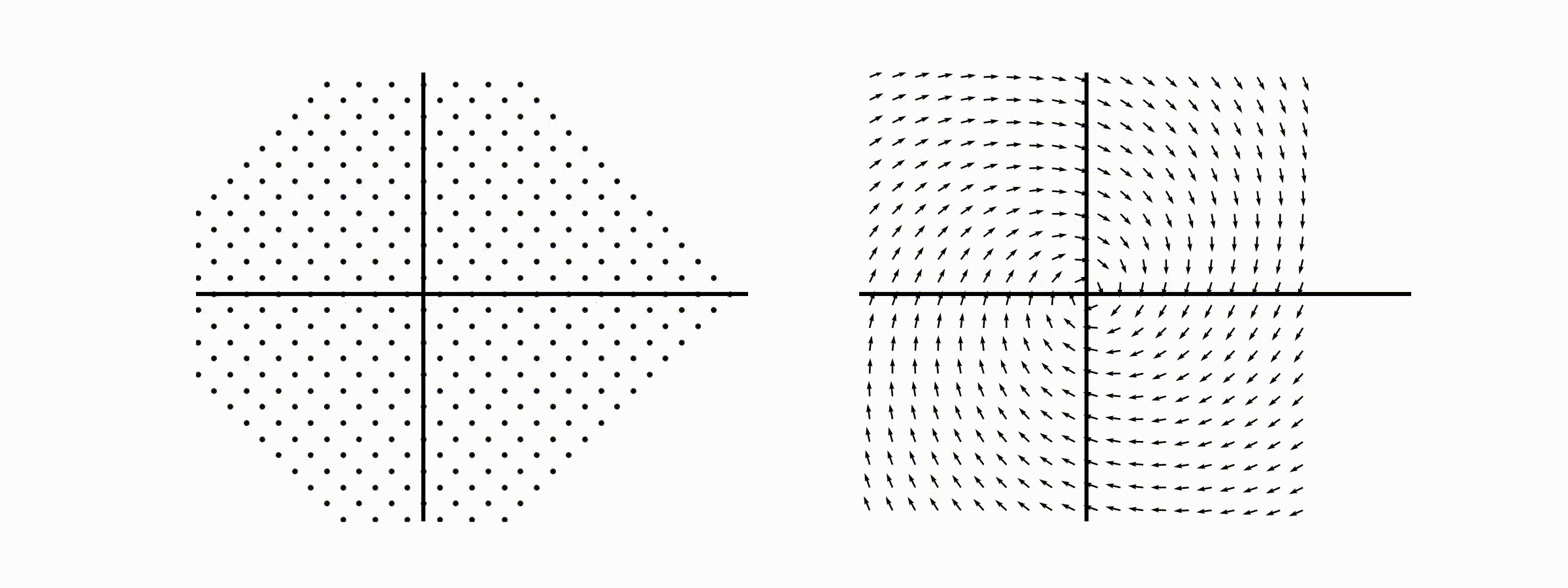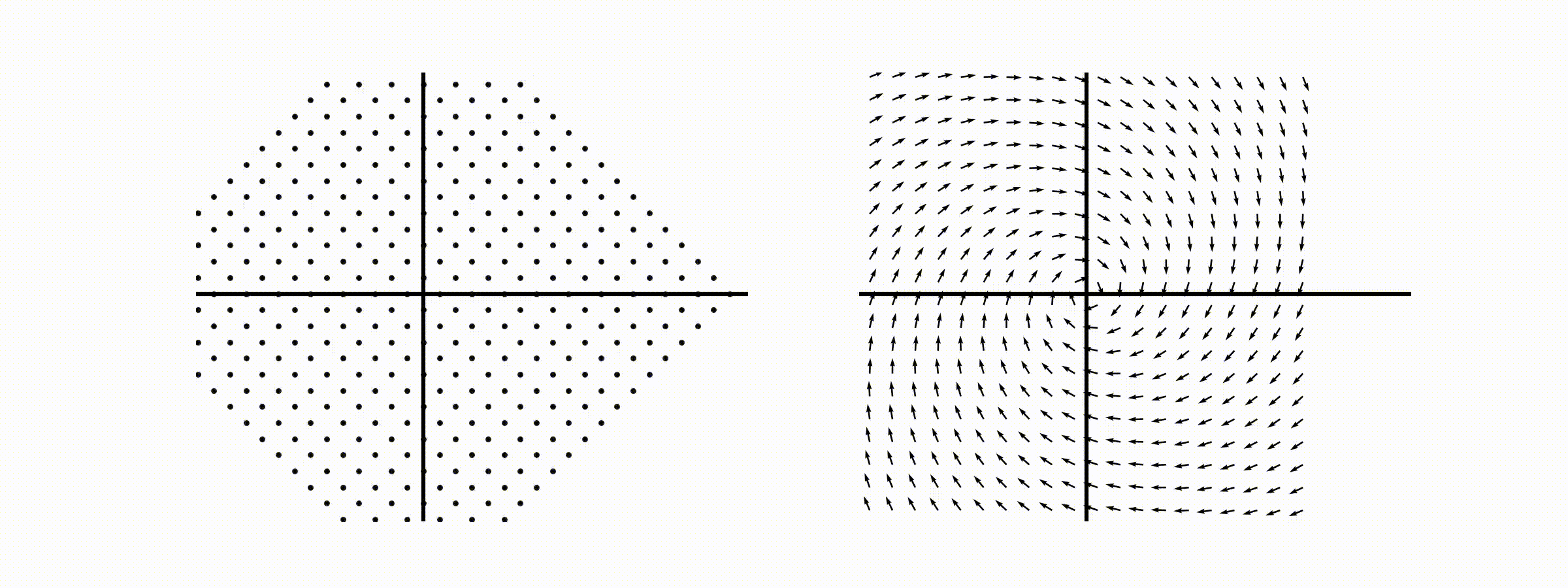
다음 몇몇 선형변환 매트리스와 그에 해당하는 Eigenvector와 Eigenvalue가 보여주는 변화를 살펴보자 egenflow1 egenflow2 egenflow3 egenflow3

                                                        ----0.3--+
                                                        |        |
                                                        V        |
+-----------------+                    +---------------------+   |
| www.daum.net    | ------ 0.2 ---   | www.naver.com       |---+
|                 | <----- 0.3 -----   |                     |
+-----------------+                    +---------------------+
     ^     |        \                     ^           |
     |     |         \                    |           |
    0.2    0.3        \                   0.15        0.3
     |     |           \                  |           |
     |     v            0.2               |           v
+-----------------+       \           +-------------------+
|                 |        \          |                   |
| www.youtube.com |         +------ |    google.com     |
|                 |<-------0.7--------|                   |
|                 |--------0.05-----|                   |
+-----------------+                   +-------------------+
\[\begin{bmatrix} daum \\ naver \\ youtube \\ google \\ \end{bmatrix} = \begin{bmatrix} 0 & 0.3 & 0.2 & 0 \\ 0.2 & 0.3 & 0 & 0.15\\ 0.3 & 0 & 0 & 0.7 \\ 0.2 & 0.3 & 0 & 0.05 \end{bmatrix} \begin{bmatrix} daum \\ naver \\ youtube \\ google \\ \end{bmatrix}\]

–>

수업 06-2 (ANN, Activation)

Week7

수업 07-1

수업 07-2

Week8

수업 08-1

Matplotlib: Python 환경에서 데이터를 시각화하는데 가장 널리 쓰이는 라이브러리 중에 하나이다. MATLAB과 유사한 환경을 제공해주는 pyplot 모듈을 활용한 인터페이스가 널리쓰인다. 아래 예시들을 함께 살펴보자.

import matplotlib.pyplot as plt
import matplotlib.pyplot as plt

x = [0, 1, 2, 3, 4]
y = [0, 1, 4, 9, 16]

plt.plot(x, y)          # 선 그래프
plt.title("Basic Line Plot")
plt.xlabel("X-axis")
plt.ylabel("Y-axis")

x = [5, 7, 8, 7, 6, 9, 5, 4, 5, 6]
y = [99, 86, 87, 88, 100, 86, 103, 87, 94, 78]
plt.scatter(x, y, color='red')
plt.title("Scatter Plot")

각 데이터 세트 (선, 점 등)에 라벨을 부여하고, 이를 레전드(legend) 함수를 활용해 그래프를 꾸밀 수 있다.

plt.plot([1,2,3],[1,4,9], label=r'$y = x^2$')
plt.plot([1,2,3],[1,2,3], label=r'$y = x$')
plt.legend() ## legend

plt.subplot을 활용해서 행렬 행태의 그래프 모임을 그릴 수 있다.

plt.subplot(1, 2, 1)  # 1행 2열 중 첫 번째
plt.plot([1,2,3],[1,4,9])
plt.title("Left")

plt.subplot(1, 2, 2)  # 두 번째
plt.plot([1,2,3],[1,2,3])
plt.title("Right")

plt환경을 조금 더 상세히 살펴보면, 두개의 오브젝트 figure와 axis를 이해할 수 있다. figure는 그림을 그리는 캔버스, axis는 그래프가 시각화되는 좌표계라 볼 수 있다.

따라서 한 Figure 안에 여러 개의 axes가 삽입될 수 있다. 아래 예제를 살펴보자.

import matplotlib.pyplot as plt

# Figure(도화지), Axes(좌표 영역) 생성
fig, ax = plt.subplots()

x = [0, 1, 2, 3, 4]
y = [0, 1, 4, 9, 16]

# ax 객체를 활용해 데이터 플롯
ax.plot(x, y, label="y = x^2", color="blue")

# 그래프 꾸미기
ax.set_title("Figure & Axes Example")
ax.set_xlabel("X-axis")
ax.set_ylabel("Y-axis")
ax.legend()
ax.grid(True)

plt.show()

NumPy의 linspace, logspace등과 결합하면 여러 1D 그래프를 손쉽게 그릴 수 있다. 예를 들어 $y=x^2$을 $x\in[-10,10]$을 그리자면

import numpy as np
import matplotlib.pyplot as plt
x=np.linspace(-10,10) # [-10,10] 범위내의 50 포인트
y=x**2 ## NumPy의 element-wise operation을 기억하자.
plt.plot(x,y)

결과를 살펴보자.

위 예제를 응용하여 아래 실습을 수행해보자. 범위 내의 아래 삼각함수를 그려보자.

예1.

\[y=\cos(\theta), \text{ with } \theta\in[-\pi,\pi]\]

예2.

\[y=\sin(\theta), \text{ with } \theta\in[-\pi,\pi]\]

예3. \(y=\tan(\theta), \text{ with } \theta\in\big[-\frac{\pi}{2},\frac{\pi}{2}\big]\)

\[x^2+y^2=10^2\] \[\varepsilon=\ln(\epsilon+1)\]

cubic crystal structure내의 결정 방위 [h,k,l]에 해당하는 단위 벡터를 그려보자. Cubic crystal의 경우 Miller index $[uvw]$가 한 결정 방향이라면 그 방향에 해당하는 벡터 $\boldsymbol b$는 아래와 같이 구할 수 있다. \(\boldsymbol b = (b_1,b_2,b_3)=\bigg(\frac{h}{\sqrt{h^2+k^2+l^2}},\frac{h}{\sqrt{h^2+k^2+l^2}},\frac{h}{\sqrt{h^2+k^2+l^2}}\bigg)\) 이를 계산하는 함수를 작성해보면

def get_direct(uvw=np.array([1,1,0])):
  """
  Argument
  --------
  uvw: as in <ndarray> or <list>

  Return
  ------
  """
  ##
  if type(uvw).__name__=='list':
    uvw=np.array(uvw)

  deno=(uvw**2).sum() # demoniator: 분모, numerator: 분자
  deno=np.sqrt(deno)
  return uvw/deno

## 테스트 해보자.
get_direct([1,1,0])
get_direct([1,1,1])

꼭 List 타입으로 주는 방식이 싫다면 아래와 같은 형태도 괜찮은 대안이 될 수 있겠다.

def get_direct(v1,v2,v3):
  """
  Argument
  --------
  v1,v2,v3

  Return
  ------
  """
  ##
  uvw=np.array([v1,v2,v3])
  deno=(uvw**2).sum() # demoniator: 분모, numerator: 분자
  deno=np.sqrt(deno)
  return uvw/deno

위 함수를 활용해 결정학적으로 같이 $[100],[010],[001],[\bar{1}00],[0\bar{1}0],[00\bar{1}]$을 3차원 그래프로 표현해보자. 3차원 점들을 표현하기 위해서는 3차원 axis가 필요하다. 이를 위해서 fig의 add_subplot 매소드에 ‘projection=3d’ 파라미터를 입력하여 3차원 axis를 만들자. 그 다음, 앞서 생성한 점들을 ‘scatter’함수를 활용해 아래와 같이 표현해보자.

%matplotlib widget
fig=plt.figure()
ax1=fig.add_subplot(111,projection='3d')
vs=[[1,0,0],[0,1,0],[0,0,1],[-1,0,0],[0,-1,0],[0,0,-1]]
for i, v in enumerate(vs):
    uvw=get_direct2(*v)
    ax1.scatter(*uvw,marker='o',color='k')

3차원 공간인지 사실 한눈에 살펴보기 어렵다. 따라서, 원점(0,0,0)에서부터 각 지점까지 화살표로 이어보는게 더 좋겠다. 화살표를 그리기 위해서 quiver매소드를 활용하였다.

%matplotlib widget
import matplotlib.pyplot as plt
fig=plt.figure()
ax1=fig.add_subplot(111,projection='3d')
vs=[[1,0,0],[0,1,0],[0,0,1],[-1,0,0],[0,-1,0],[0,0,-1]]
orig=[0,0,0]
for i, v in enumerate(vs):
    uvw=get_direct2(*v)
    ax1.scatter(*uvw,marker='o',color='k')
    ax1.quiver(*orig,*uvw,arrow_length_ratio=0.2,color='r')

3차원 방향을 좀 더 명확히 살펴보기 위해, 반지름 1인 구(sphere)를 같이 그려보면 좋겠다. 이를 위해서는 구면 좌표계(spherical coordinate system)를 활용하면 더욱 쉽게 구를 그릴 수 있다. $(r,\theta,\phi)$의 좌표계에서 $r=1$로 고정하면, 반지름이 1인 구의 면에 해당한다. 아래 범위 내의 경우를 활용하면 되겠다.

주어진 구 좌표계는 다음과 같이 직교 좌표계 $(x,y,z)$로 아래와 같이 변환된다.

np.mgrid기능을 활용하면 쉽게 그리드를 만들 수 있다. np.linspace와 유사하나, 다차원으로 확장가능하며, grid를 만들기에 적합하다.

import numpy as np
theta,phi=np.mgrid[0:np.pi:10j,0:2*np.pi:10j]

위에 만들어진 theta와 phi를 직교좌표계로 바꾸면

import numpy as np
theta,phi=np.mgrid[0:np.pi:10j,0:2*np.pi:10j]
r=1 # radius가 1이다.
## 직교 좌표계로 아래와 같이 변환할 수 있다.
x=r*np.sin(theta)*np.cos(phi)
y=r*np.sin(theta)*np.sin(phi)
z=r*np.cos(theta)

이제 grid된 x,y,z좌표와 matplotlib의 plot_wireframe을 활용해서 3D 구면을 그려보자.

import numpy as np
theta,phi=np.mgrid[0:np.pi:10j,0:2*np.pi:10j]
r=1 # radius가 1이다.
## 직교 좌표계로 아래와 같이 변환할 수 있다.
x=r*np.sin(theta)*np.cos(phi)
y=r*np.sin(theta)*np.sin(phi)
z=r*np.cos(theta)

fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
ax.plot_wireframe(x,y,z,alpha=0.2,lw=0.9) ## alpha: 투명도, lw: linewidth

나아가, 그 위에 앞서 구한 결정방향들을 올려보자.

import numpy as np
theta,phi=np.mgrid[0:np.pi:20j,0:2*np.pi:20j]
r=1 # radius가 1이다.
## 직교 좌표계로 아래와 같이 변환할 수 있다.
x=r*np.sin(theta)*np.cos(phi)
y=r*np.sin(theta)*np.sin(phi)
z=r*np.cos(theta)

fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
ax.plot_wireframe(x,y,z,alpha=0.2,lw=0.9)

##
vs=[[1,0,0],[0,1,0],[0,0,1],[-1,0,0],[0,-1,0],[0,0,-1]]
orig=[0,0,0]
for i, v in enumerate(vs):
    uvw=get_direct2(*v)
    ax.scatter(*uvw,marker='o',color='k')
    ax.quiver(*orig,*v,arrow_length_ratio=0.2,color='r')

그런데 사실, 3차원으로 그린 그래프 툴이 개발되기 전에도 많은 재료공학자들이 3차원 정보를 표현해야만 했다. 그들은 3차원 정보를 2차원면에 표현하기 위해 stereographic projection법을 활용하였다.

%matplotlib widget
#%matplotlib inline
fig=plt.figure()
ax1=fig.add_subplot(111,projection='3d')
vs=[[1,0,0],[0,1,0],[0,0,1],[-1,0,0],[0,-1,0],[0,0,-1]]
orig=[0,0,0]
for i, v in enumerate(vs):
    uvw=get_direct2(*v)
    ## quiver 메소드를 활용하였다.
    ax1.quiver(*orig,*v,arrow_length_ratio=0.2,color='r')

d=1.2
ax1.set_xlim(-d,d)
ax1.set_ylim(-d,d)
ax1.set_zlim(-d,d)

Crystal symmetry

수업 08-2 (np.meshgrid, np.mgrid, grid, contouring)

Week9

수업 09-1 (Force vs. displ 데이터 -> 응력 선도)

\[\sigma=k\varepsilon^n\]

적절한 k값과 n값을 앞서 calibration sheet의 $ a$ 그리고 $ b $에 해당하는 값을 찾기 위해서는 $\log$ 함수의 활용이 유용하다.

\[\log\sigma=\log k + n\log \varepsilon\]

밑(base)이 자연수(2.713…)인 로그 함수를 활용한다면

\[ln\sigma=\ln{k}+n\ln\varepsilon\]

이를 활용해 적절한 $k$ 값 및 $n$ 값을 구해보자.

# np.log 함수를 활용해 밑이 자연수인 로그 함수를 활용하자.
# np.log(sigma), np.log(epsilon)
# plt.plot 활용해 직선 그려보기
# a값 그리고 b값 찾기.
# log (a) 그리고 log (b)로부터 a, b값을 역산(거꾸로 계산) 해보자.

수업 09-2 (노이즈가 있는 데이터로부터 최소자승법을 활용한 선형회귀)

Week10 (Matplotlib + Hall-petch equations, Creep data)

수업 10-1 (Creep data)

수업 10-2 (Contouring)

Week11

수업 11-1 (무게비 원자비 변환)

수업 11-2

Week12

수업 12-1

수업 12-2

Week13

수업 13-1

수업 13-2

Week14

수업 14-1

import numpy as np
import matplotlib.pyplot as plt

# 예제: 금속 합금 조성(Cu %) vs 전기 전도도
x = np.array([0, 5, 10, 15, 20])
y = np.array([58, 55, 50, 45, 42])  # 전도도 W/mK

plt.scatter(x, y, color='b', label='Data')
plt.xlabel("Cu content [%]")
plt.ylabel("Electrical Conductivity [W/mK]")
plt.title("Conductivity vs Cu content")
plt.grid(True)
plt.legend()
plt.show()

수업 14-2

Week15 (기말고사)

수업 15-1

수업 15-2

Enjoy Reading This Article?

Here are some more articles you might like to read next:

  • NIST 교환 학생 소식
  • 2025 July, NUMISHEET 학회 참석 및 발표
  • 2024 July, LANL 방문
  • a post with tabs
  • a post with typograms