Click this link to use on-line Google spreadsheet.

You can also download the microsoft Excell spreadsheet: link

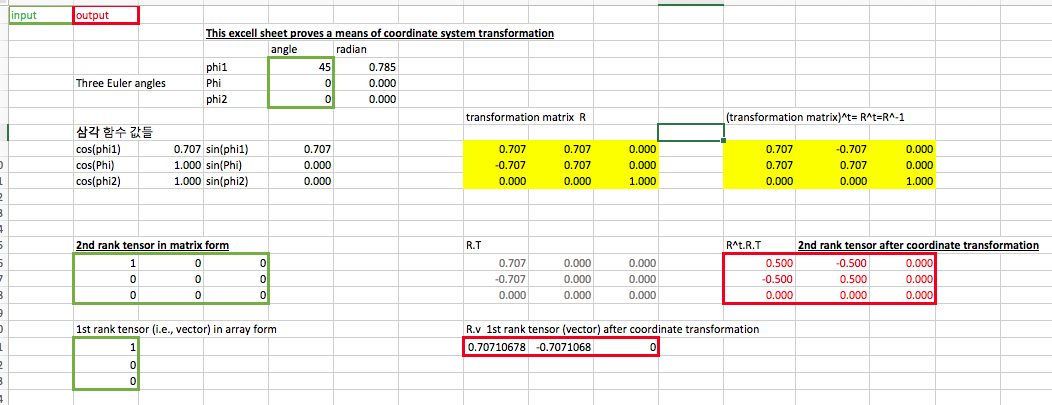
Above is a captured image of the spread sheet.

This sheet allows you to put three Euler angles to obtain transformation matrix. You can also put 2nd rank tensor (and/or 1st rank tensor, i.e., a vector) in a matrix form and obtain the one after the coordinate transformation is applied.

Namely, you obtain the transformation using the transformation rule for the 2nd rank tensor. For example, a 2nd rank stress tensor \(\sigma\) is transformed to a new coordinate system, which results in \(\sigma^\prime\) by applying the transformation matrix \(R\) as below:

\[\sigma^\prime_{ij} = R_{ik} \sigma_{kl} R_{jl} \\\]

We can obtain the trasnformation \({\bf R}\) as a function of three Euler angles (\(\phi_1,\Phi,\phi_2\)) - look for more about Euler angles here.

Note that in the Excel, the summation is performed using MMULT function.